1. Introduction
In recent years, significant advancements have been made in the field of artificial intelligence (AI), enabling intelligent systems to excel in various fields. Strategic board games have long served as popular test beds for evaluating the capabilities of AI algorithms, including groundbreaking achievements like Alpha-Go. Among these games, Reversi, also known as Othello, presents a complex and challenging environment for AI systems to demonstrate their decision-making prowess. This paper is going to focus on the application of AI techniques, including greedy algorithms, Minimax, alpha-beta pruning, and game theory principles, to enhance the performance of AI systems in playing Reversi.
Reversi is a two-player board game, involves placing and flipping pieces with the objective of gaining the majority of the board. Its simplicity, well-defined rules, and strategic depth make it an ideal choice for studying AI algorithms. While techniques like Minimax and alpha-beta pruning have been widely applied in AI for various strategic board games, the utilization of greedy algorithms in this context has received less attention. Greedy algorithms aim to make locally optimal choices at each step, exploiting immediate gains. On the other hand, Minimax allows the AI to evaluate future positions by considering a certain depth of the game tree and alternating between maximizing its own score and minimizing the opponent's score. And by using alpha-beta pruning, we can enhance the efficiency of the Minimax algorithm, reducing the number of explored nodes and improving decision-making speed.
This research aims to reveal the potential benefits and limitations of applying greedy algorithms in gaming scenarios, specifically through a comparison with the Minimax algorithm. This paper aims to reveal whether the utilization of greedy algorithms can lead to increased victories for AI players. By exploring the effectiveness of various techniques in Reversi, we can better understand their applicability in the strategic domain and contribute to deeper and more detailed research on the role of AI in game theory.
2. Different AI strategies
Early game theory can be traced back to [1]. In this section, three distinct Reversi AI algorithms (random move algorithm, Greedy Algorithm, Minimax algorithms with alpha-beta pruning) will be mentioned, and each is designed with different move stragy. The objective of this section is to offer an understanding of the logic and implementation of these algorithms. Pseudocode will be presented in the figures to facilitate comprehension.
2.1. Random move algorithm
In the below pseudocode:
// Pseudocode: randomMoveAlgorithm
function randomMoveAlgorithm(board, currentPlayer):
validMoves = get all valid move positions
If validMoves is empty:
return
randomIndex = generate random integer between 0 and length of validMoves - 1
randomMove = validMoves[randomIndex]
row = randomMove.row
col = randomMove.col
place currentPlayer’s piece at board[row][col]
The “random Move Algorithm” function iterates through all the available positions to make a move and selects one position randomly. It first checks if there are any valid move positions. If there are, it generates a random index within the range of valid moves and selects the corresponding move. Then, it retrieves the row and column of the randomly selected move and places the current player's piece at that position on the board.
This random move algorithm doesn't evaluate the current state of the game and lacks competitiveness, but it provides a simple and quick way for the AI to make a move without spending time on board evaluations. It is commonly used in the simplest difficulty level of AI for the game of Reversi.
2.2. Greedy algorithm
At each turn, the algorithm aims to maximize the number of opponent's pieces that can be flipped. However, if a move is possible in one of the four corners of the board, the AI will add a higher score on it.
In the code below,
// Pseudocode: evaluateMove
function evaluateMove(board, row, col, currentPlayer):
flippedCount = 0
for each direction in all directions:
count = 0
find all pieces can be flipped
if piece can be flipped:
flippedCount += count
if (row, col) is a corner position:
flippedCount += 10 // Add a higher score for corner positions
return flippedCount
The the “evaluateMove” function is responsible for evaluating a specific move position on the board. It calculates the scores by considering the number of opponent's pieces that can be flipped by making that move. It iterates through all possible directions from the given position. For each direction, it checks how many of the opponent's pieces can be flipped by extending in that direction. It counts the number of opponent's pieces that can be flipped and adds it to the “flippedCount”. Additionally, if the move position is in the corner of the board, it adds a higher weight to the “flippedCount” to prioritize corner moves. The “evaluateMove” function then returns the “flippedCount” as the evaluation score for that move position.
Then in the “ai2MakeMove” function,
// Pseudocode: ai2MakeMove
function ai2MakeMove(board, currentPlayer):
validMoves = get all valid move positions
if validMoves is empty:
return
bestMove = validMoves [0]
maxScore = -infinity
for each move in validMoves:
row = move.row
col = move.col
score = evaluateMove(board, row, col, currentPlayer)
if score > maxScore:
maxScore = score
bestMove = move
Place currentPlayer’s piece at bestMove.row, beatMove.col
This function is responsible for the AI's decision-making process to select the best move position to play. It starts by obtaining all valid move positions available for the current player on the board. If there are no valid moves, the function exits. Otherwise, it initializes variables “bestMove” and “maxScore” to track the move with the highest score. It then iterates through each move position. For each move, it calls the “evaluateMove” function to calculate the score of that move position. If the calculated score is higher than the current “maxScore”, it updates the “maxScore” and sets the current move position as the “bestMove”. After evaluating all the available moves, the function selects the “bestMove” and places the current player's piece at that position on the board.
2.3. Minimax algorithms with alpha-beta pruning
2.3.1. Minimax. The minimax algorithm is originally from the Park-McClellan algorithm, published by James McClellan and Thomas Parks in 1972 [2]. Minimax is a widely used decision-making algorithm in game theory and AI. It is particularly suitable for turn-based games like Reversi. “Minimax is used to identify the best moves in a game tree generated by each player’s legal actions. Terminal nodes represent finished games; these are scored according to the game rules.”[3]. The Minimax algorithm considers the game as a zero-sum competition between two players: one player maximizes their own score, while the other minimizes it. By recursively evaluating possible moves and their consequences on the game state, the AI can anticipate the opponent's responses and select the most advantageous move. “For any game, we can define a rooted tree (the "game tree") in which the nodes correspond to game positions, and the children of a node are the positions that can be reached from it in one move.” [4]. The depth of the game tree search determines the level of strategic analysis performed by the algorithm, as shown in figure 1.
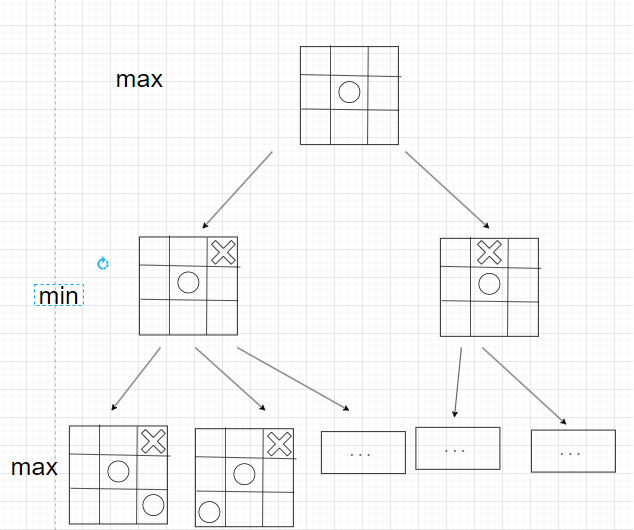
Figure 1. An example of minimax search tree in Tic Tac Toe.
2.3.2. Alpha-beta pruning. Alpha-beta pruning is an optimization technique applied to the Minimax algorithm to reduce the number of nodes evaluated during the search process. It eliminates the evaluation of certain branches that are guaranteed to be less optimal, thus significantly reducing the time cost. By maintaining upper and lower bounds, known as alpha and beta, the algorithm prunes branches that cannot possibly affect the final decision. “Alpha-Beta Pruning is a good optimization of Minimax because achieves the same results using less time and memory, as less moves and less states are evaluated.” [5]. This pruning technique allows the AI to explore a deeper depth of the game tree in less time, as shown in figure 2 [6].
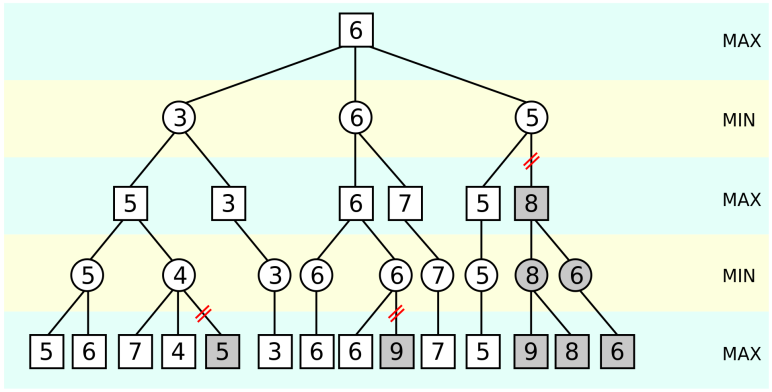
Figure 2. An illustration of alpha-beta pruning.
3. Evaluation
This section will have two subsections: Test and test result. The test section will cover research methods, research objects, and research tools. The test result section will show the data of the test in figures. Simple analysis will also be included.
3.1. Test
To evaluate and compare the performance of the three different AI algorithms, a series of AI versus AI matches were conducted. The objective was to assess their gameplay strategies, decision-making abilities by measuring their average execution time and win rates.
In these conducted multiple matches, each algorithm played against the other two algorithms in black and white. In these multiple games, each algorithm is played against the other two algorithms 1000 times in black and white, and the winning percentage and average running time between different algorithms will be recorded.
All matches were played on a 6x6 Reversi board. Relevant codes and experiments will be carried out in a C++ environment
3.2. Test result
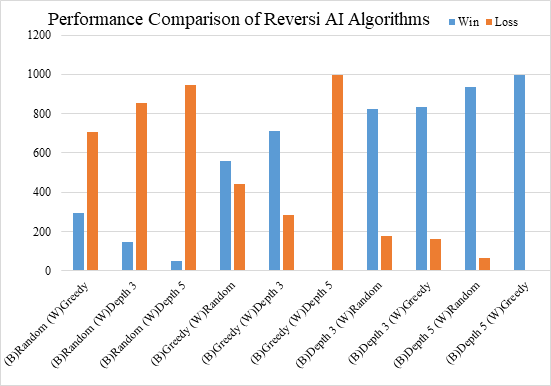
Figure 3. Performance comparison of each algorithms.
According to figure 3, the notation “B” and “W” means the AI are holding black and white pieces, Depth X indicates the depth of this minimax tree is X. For example, (B)Depth 3 means the AI setting as the depth 3 minimax algorithms is holding black piece.
According to the data in figure 6, the minimax algorithms shown a majority of winning, especially as depth increases. The greedy algorithm has shown a major advantage in playing against random algorithms. When holding black pieces, weak advantage is shown when against depth 3 minimax algorithms, but disadvantage when holding white pieces. In general, the greedy algorithm can maintain a win rate of 44% against minimax opponents in depth 3. However, as the depth increases, the Greedy Algorithm loses its competitiveness, and its win rate dramatically drops to less than 1%.
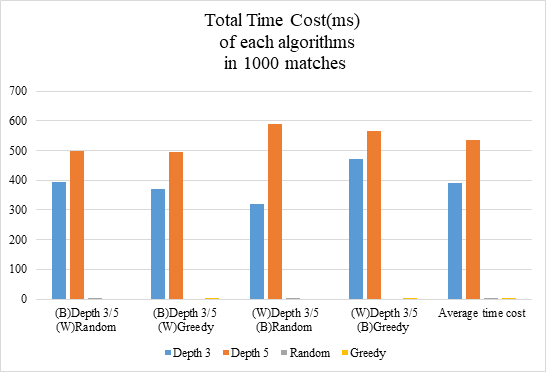
Figure 4. Running time of each algorithms.
According to figure 4, the total runtime of each algorithms in each 1000 matches is shown in millisecond(ms). The runtime of minimax algorithm is increasing with depth, the average runtime time increase by 37.7% as the depth change from 3 to 5, which the minimax algorithm in depth 3 has average runtime in 389.88ms, depth 5 has average runtime in 536.95ms. Random and Greedy algorithms perform great in the runtime test with both of them have a average runtime less than 2ms.
4. Conclusion
The research conducted in this study addressed the question of whether the application of Greedy Algorithms can lead to increased victories for AI players in gaming scenarios, compared to the Minimax Algorithm. Based on the research findings presented in this paper, it can be concluded that the Greedy Algorithm, although efficient in terms of execution time, does not perform better than the Minimax Algorithm, especially when the searching depth of Minimax is increased. The results indicate that the Greedy Algorithm is not a highly intelligent strategy in competitive scenarios, where the Minimax Algorithm with a deeper searching depth showcases superior performance. “The AI preformed much better the more it looked ahead versus looking for moves valuable in the short term.” [7].
However, it is worth noting that the Greedy Algorithm does possess certain advantages. One of its strengths lies in its low computational time, allowing for quick decision-making. In comparison to the Random Algorithm, the Greedy Algorithm gains more victories overall while maintaining a similar execution time.
In conclusion, the findings of this study indicate that the Greedy Algorithm is not a superior alternative to the Minimax Algorithm in competitive scenarios, particularly with increased searching depth. However, its advantage lies in its reduced computational time, making it a viable option for scenarios where time efficiency is prioritized. It is important to further refine and enhance the algorithmic strategies in order to develop more effective AI systems for strategic decision-making in various gaming scenarios. For future research, concentrating on improving the performance of the Greedy Algorithm by incorporating more advanced heuristics or adaptive strategies maybe a good choice. Additionally, combining the strengths of both the Greedy Algorithm and the Minimax Algorithm could be a promising direction for further investigation.



