Research on multi-path optimization problem based on particle swarm optimization algorithm

1. Introduction

1.1. Particle Swarm Optimization algorithm

Particle swarm algorithm, also known as particle swarm optimization algorithm or bird swarm foraging algorithm (Particle Swarm Optimization), abbreviated as PSO. PSO is a new evolutionary algorithm. The theory was introduced by Dr. Eberharter and Dr. Kennedy in 1995. This theory stems from the study of the hunting behavior of birds. PSO simulates this scenario and uses it to solve optimization problems. What is the strategy for finding food? The most effective way is to follow the bird that finds the most significant piece of food. The food gets bigger the closer you get, and no bird knows where the center of the food is. Then, the best flocks of birds look for food in an area. There are some small pieces of food near the food center. Usually, birds away from the center will cooperate socially with their neighboring birds to find food. Particle swarm optimization algorithm (PSO) is a swarm intelligence optimization algorithm developed by simulating the foraging behavior of birds and fish schools. It is similar to the genetic algorithm. It starts from a random solution, finds the optimal solution through multiple iterations, and evaluates the quality of the solution through the fitness function. Because of its simplicity and ease of implementation, it has become an effective optimization tool for many optimization problems. Based on the observation of animal cluster activities, the particle swarm algorithm regards the solution space of the problem to be optimized as a multi-dimensional space, and each solution is regarded as a moving particle in the space. On this basis, this project proposes a multi-objective optimization algorithm based on genetic algorithm, which can effectively control the dynamic evolution of the population by sharing among the members of the population [1].

The advantages of the PSO algorithm are its simple principle, easy implementation and higher search efficiency when solving some complex problems. Therefore, the PSO algorithm has great application potential in path optimization problems.

In view of the shortcomings of the particle swarm optimization algorithm, which easily falls into local extremes and has limited search space, quantum theory is combined with the particle swarm optimization algorithm, and the quantum particle swarm optimization algorithm is used to solve the multi-machine collaborative target allocation problem. The particles in the quantum particle swarm optimization algorithm are represented by vectors, composed of each allocation plan in the multi-machine cooperative target allocation problem, thereby searching for the optimal solution in the solution space. Simulation shows that this algorithm has fast convergence speed and good global convergence performance and is more suitable for solving target allocation problems.

1.2. Game two-dimensional space multi-path optimization

In order to simplify the description, this article directly uses the two-dimensional space of the game map as the search domain, and considers the path optimization problem of NPC movement on the two-dimensional plane map. Given the starting point, end point and various game obstacles on the plane, the goal is to avoid Find the shortest path from the starting point to the end point without obstacles [2].

2. Methodology

2.1. Particle swarm optimization algorithm steps

According to the principle of the PSO algorithm, the algorithm needs to be designed to initialize the particle group, set boundary conditions, calculate individual fitness, calculate the optimal position of the individual and the group, update the individual fitness, update the optimal position of the individual and the group, judge the termination condition, and output the optimal. The main parts such as optimization and solution [3], the detailed process is as follows (Fig 1):

Figure 1. Detailed process

2.2. Initialization and boundary conditions

In the PSO algorithm, a particle population is first randomly initialized, including several movable particles. The particles start from the initial position, have a certain speed, and move in a certain limited space in a random direction. The position cannot exceed the space. At the boundary, the speed cannot be too high, and obstacles in the space are also inaccessible locations [4].

Assume that in the two-dimensional search space, there are N particles forming a community, where the \( i-th \) particle is represented as a two-dimensional vector:

\( {X_{i}}=({x_{i1}}{,x_{i2}}) \)

The speed of the \( i-th \) particle is also a two-dimensional vector, expressed as:

\( {V_{i}}=({v_{i1}}{,v_{i2}}) \)

2.3. Fitness function

The fitness function is an important concept in the PSO algorithm. Different problems require the design of different fitness functions. In this problem, we can use the objective function of the problem as the fitness function, that is, using the particle position to the endpoint. This is expressed in terms of distance and is used to estimate the current position of the particles. Smaller values indicate higher fitness, and vice versa [5].

2.4. Particle position and velocity

The position of the particles reflects the solution to the problem, and the velocity of the particles reflects the speed of the particles in the scheme. The trajectory of particles can be expressed by space vector or velocity vector. In each iteration, the location and rate of the particles will be modified according to some law.

2.5. Speed and position update rules

The particle speed and position update rules are the core part of the PSO algorithm [6]. In each iteration, the speed of the particle will be updated according to the following formula. When the \( i-th \) particle of the \( t-th \) generation evolves to the \( t+1-th \) generation, it will be updated according to the following formula:

\( {v_{i}}(t+1)=w∙{v_{i}}(t)+{c_{1}}{r_{1}}(t)[{p_{i}}(t)-{x_{i}}(t)]+{c_{2}}{r_{2}}(t)[{p_{g}}(t)-{x_{i}}(t)] \)

Among them, \( v\_i \) is the rate of particle \( i \) , \( w \) is the inertia weight, \( c\_1 \) individual learning coefficient, \( c\_2 \) is the group learning coefficient, \( r\_1 \) and \( r\_2 \) are random values in the [0,1] interval, used to increase the randomness of particle motion, \( p\_i \) is the individual optimal position of particle \( i \) , \( x\_i \) is the current position of particle \( i \) , and \( p\_g \) is the global optimal position.

The particle’s position is updated according to the following formula:

\( {x_{i}}(t+1)={x_{i}}(t)+{v_{i}}(t+1) \)

2.6. Individual optimality and global optimality of particles

In this method, each particle has a separate optimal position, which represents the optimal position encountered by the particle during the search process [7]. In addition, the entire particle swarm also has a global optimal position, which represents the optimal position that all particles in the particle swarm have encountered. Using the group’s optimal position is a manifestation of the group intelligence of the PSO algorithm. In each iterative process, the corresponding genetic algorithm will be used to optimize. When the fitness of the new positioning is higher than the original positioning value, the new positioning is the best positioning, on the contrary, the positioning is not done.

2.7. Termination condition

Particle swarm optimization usually ends under certain ending conditions. These termination conditions can include reaching the maximum number of iterations, the fitness value reaching a preset threshold, and the fitness no longer changing after \( n \) generations, etc. After the terminal condition is satisfied, the method outputs it to the optimal value in the form of the optimal solution.

3. Experimental tuning

There are three parameters that need to be adjusted in the PSO algorithm, namely inertia weight, individual learning factor and group learning factor. The three parameters work together to affect the speed and effect of algorithm convergence.

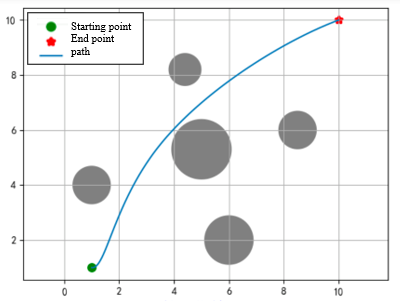
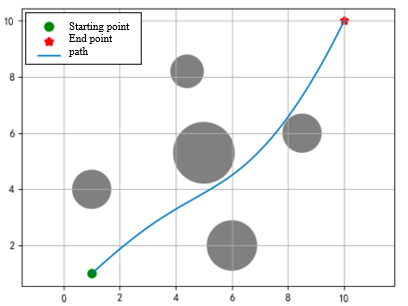
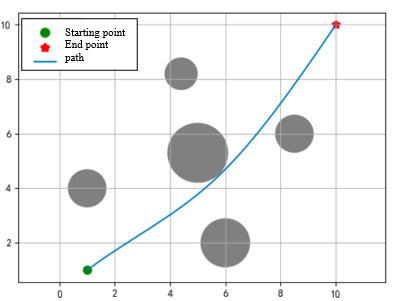
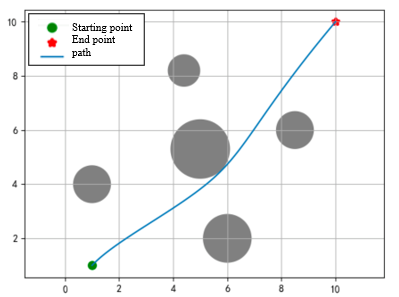
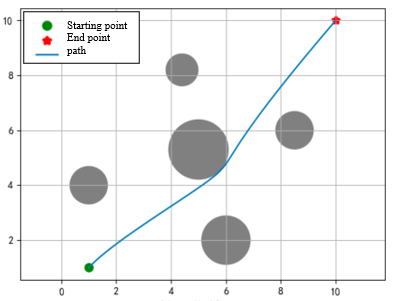
The experimental map is set to a plane of size \( 10*10 \) . The starting point is set at coordinates \( (1, 1) \) , and the end point is set at coordinates \( (10, 10) \) . In order to increase the difficulty, 5 different positions are set between the starting point and the end point. Obstacles are represented by circular areas. The goal is to use the PSO algorithm to find an optimal path from the starting point to the end point while avoiding the obstacles in the picture.

Theoretically, the greater the number of particle groups and evolutionary generations, the better, but at the same time it will also reduce the economy. After considering the economy and actual effects, the experiment finally set the number of particle groups to 500, evolved for 30 generations, and the individual learning factor and the group learning factor are set to 1.5, the maximum inertia weight is set to 0.9, and the minimum is set to 0.4. A dynamic adjustment method of high in the early stage and low in the later stage is adopted. During initialization, the first particle path is set as a straight line from the starting point to the end point, and other particles randomly generate paths. point, the initial speed is randomly generated, and through continuous optimization of the PSO algorithm, the optimal path between the starting and ending points is finally found. The experimental effect is as Figure 2.

Figure 2. Path planning based on particle swarm optimization

The obstacle coordinates represented by the largest circle in the middle are at (5.0, 5.3), slightly above the diagonal center line. The path shown before the 10th iteration is a local optimum. After that This local optimum was successfully skipped through calculation. After the 20th time, there are relatively few changes in the graphics, just fine-tuning on the optimal path.

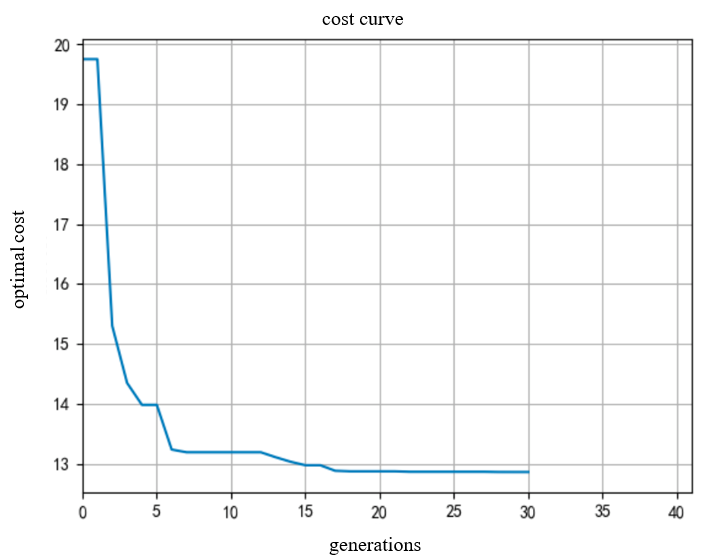
Figure 3. Cost curve

The above Figure 3 shows the change process of the objective function value from large to small during the 30 iterations, and tends to be stable after about the 17th generation, which is consistent with the conclusion drawn from the graphical display.

4. Conclusion

The experimental results show that the PSO algorithm has the advantages of simple principle, simple realization, and few parameters. The convergence speed will slow down in the later stage of iteration. Parameters also need to be adjusted in the two-dimensional space to prevent convergence to the local optimum.

The parameters of the standard particle swarm algorithm are fixed. \( w \) describes the “inertia” of the particles. The value can be between 0.4 and 0.9. In the early stage of evolution, in order to ensure that each particle can maintain its own movement and enough space to search, the \( w \) value should be large. In the later setting, \( w \) should be larger. Smaller, learn more from other particles. If \( w \) is too large, it will easily lead to the fact that even if other particles find better ones, the current particle’s inertia is too large and cannot move to the optimal position quickly. It will move towards the individual extreme value and the global extreme value respectively. Step size, the value can be between 0.1 and 2. It should be larger in the early stage and larger in the later stage, so as to balance the global search ability and local search ability of the particles. There is a tradeoff between global optimization and local optimization of particle swarm. The three parameters jointly affect the movement direction of the particles.