Finding the best opening in chess with multi-armed bandit algorithm
University of Virgina, Virginia, 22903, USA
mzu4dm@virginia.edu
Abstract. With many gaming AI being developed and being able to defeat top human players in recent years, AI has once again become the hottest topic in research and even in our daily life. This paper also researches on gaming AI and chess. Instead of using deep learning and the Monte Carlo Search algorithm, this paper focuses on the opening only with multi-armed bandit algorithms to find the best moves and opening. Specifically, the method used in this paper is epsilon greedy and Thompson sampling. The dataset used in this paper is from Kaggle. This paper considers each move as a set of choices one needs to make and considers the big picture as a multi-armed bandit problem. This paper aims to develop a relative best strategy to counter those opening or make changes to a disadvantaged situation.
keywords: multi-armed bandit, chess, epsilon greedy, Thompson sampling.
1. Introduction
Artificial Intelligence is a challenging research topic. The early research on Artificial intelligence focuses on competitive games. These competitive games are good ways to determine the intelligence level of the machine [1]. Thus, increasing the intelligence level of the machine becomes the hottest topic in the research of competitive game of machines. In recent years, AI has developed, such as AlphaGo, which was already able to compete and defeat the top human players in the world. With this news, AI got the world's attention and reached unprecedented popularity.
Nowadays, the game of machines mainly focuses on the deep neural network and uses neural networks to study the existing experience. After the neural network gains experience from each game, it changes its parameters and outputs its best strategy [2]. AlphaGo gained rich experience from the human Go master. When AlphaGo plays a game, it will use those experiences to make decisions like human Go masters. However, AlphaGo Zero is based on the basic rule of Go and uses deep learning and Monte Carlo Tree Search. After 3D self-gaming, it defeats the last version of AlphaGo. Besides Go, it has also achieved the level that humans cannot reach on other board games, such as chess and Shogi [3].
AlphaGo was developed in 2016. The AI of chess even has a longer history. Chess is one of the most popular and well-known board games in the world. The goal of the game is to use your "army" to checkmate your opponent's king while the king has nowhere to run. Different pieces have different advantages and limits on their move. Researchers also start to develop competitive AI very early, and they already developed AI that is able to defeat human chess master Kasparov in 1997 [4].
The research on AI in board games already achieved huge success. It shows people cutting-edge technology in computer science and the potential of AI. This paper uses a different approach to investigate the theories in chess. Instead of gaining experience from each game, this paper only focuses on the opening strategy. The algorithms used in this paper are the epsilon greedy algorithm and Thompson sampling. Multi-armed bandit algorithms explore the data and find the best mean reward of all moves. Finally, it generates a relatively good strategy for the opponent's opening. With the result of this research, one can gain a deep understanding of the theory of chess, such as how to counter the opponent's strategies or how people make a difference in their current strategies when their opening is disadvantaged to their opponents.
2. Basics analysis of dataset
2.1. Chess background
Chess is an abstract strategy game with observable characteristics, which means the player can know the information of both sides. It starts with a board that has eight by eight grids and the grid arrangement is black and white intertwined. The bottom left grid must be black. The chess pieces are arranged in the same way each time. From up to down, the first two rows are all black pieces and the last second rows are all white pieces. The second row and the second last row are filled with pawns. The first row and last row are arranged in the order of rook, knight, bishop, queen, king, bishop, knight, and rook.
Each piece has different ways to move which gives each of them different strategic significance. Besides obeying these rules to move, capture pieces, and checkmate the opponent, there are two additional rules to move. One of them is castling. It can only happen when there are no pieces in between, the king and rook have not moved prior, and the king is not being checked. The other one is transforming, when a pawn reaches the other side of the board, it can transform into any piece but the king.
The move of chess can be recorded easily. The board is placed at the white side's perspective and is considered as a co-ordinate. The y-axis is 1 to 8 and the x-axis is a to h for each grid. The upper case of the name of each piece is used to represent each piece. The lower case of a character plus a number is used to represent the location the piece moved to. For example, Qd3 means move the queen to d3. The knight is represented by N because K is already taken by the King. The pawn is a special case that only the location is enough, such as e4 means the pawn move to e4. The transforming of a pawn is represented by the location plus "=" plus the piece that transforms into. If the move captures a piece, an "x" is put between the piece and the location. If a pawn is making a capture, a lowercase character is used to represent the file it is moving from. If the move is a check, a "+" should be added at last. If the move is checkmate, add a "\#" at last. Sometimes, the representation might be ambiguous for the same two pieces in the same rank. For example, Rd1 could mean any one of the rooks. In this case, the file the piece is moving from is recorded and placed after the letter that represents pieces. Similarly, if two pieces are in the same file, the rank will be recorded in the same way as the previous case do. Finally, the castle can be recorded by "O-O" for the kingside and "O-O-O" for the queenside. Since the white side always moves first, these representations are enough to show all of the cases of what's going on.
2.2. Basic analysis of dataset
Before applying the bandits algorithm to the dataset, some data cleaning needs to be done to extract the most important information. First, the ids are not helpful to the chess game, so this study first drop the features about id which include "id", "black\_id", and "white\_id". In addition, the start and end times are not helpful, so the features "created\_at" and "last\_move\_at" are also dropped. At last, the quickest way possible to win is the fool's mate, which takes two turns to checkmate. The "turn" in the dataset are total moves, so the games that have "turn" less than 3 are meaningless and need to be dropped.
After the data is cleaned, we can get some basic information and strategies from the dataset without any algorithm. First, this study extracts the first move of white and get the 3 most common first moves white will take.
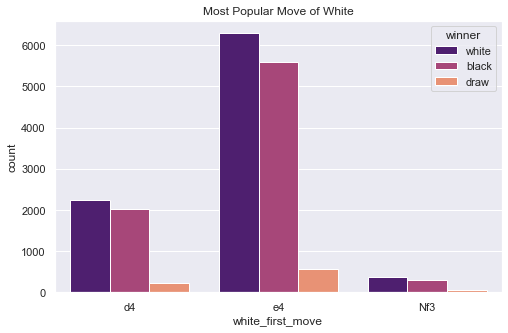
Figure 1. The most popular move of white top 3.
As can be seen from Figure 1, white usually moves the pawn from columns d and e by two-step ahead. E4 is the most common one and is much more common than other moves. D4, the second common move, is only one-third of the people who take e4 as first. The third common move is Nf3. Even though it is the third most common move, there are already very few people who will make this move.
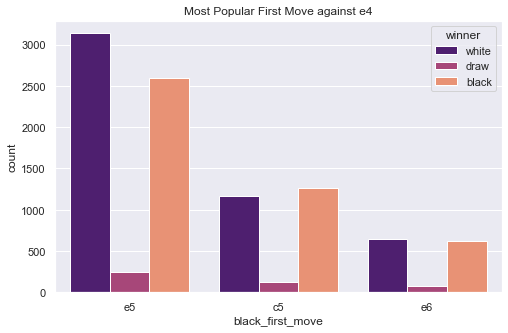
Figure 2. Most popular move for black to against white’s e4.
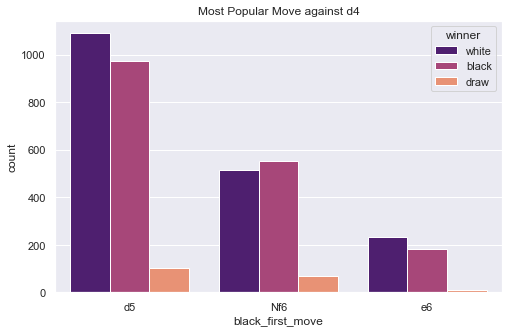
Figure 3. Most popular move for black to against white’s d4.
Referring to Figure 2 and Figure 3, for the black side, the most common move to counter e4 is e5, c5, and e6. To counter the d4, players will usually take d5, Nf6, and e6 as their moves.
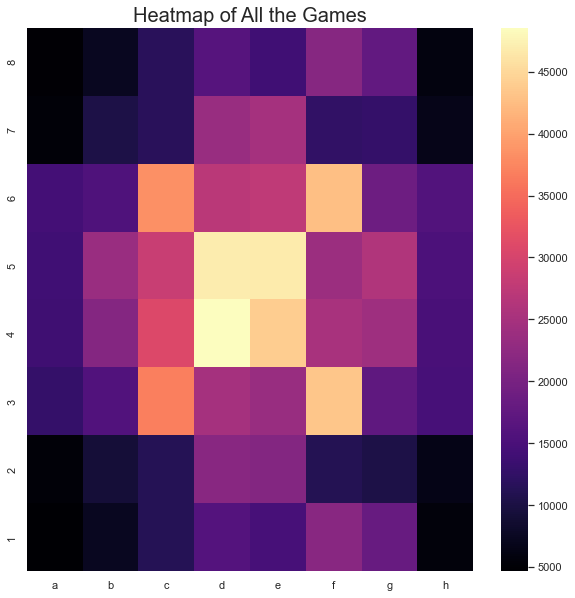
Figure 4. Heat maps for all the move in All the game.
From the heat map (Figure 4), we notice that most of the moves ended at the center of the board. And not much move will end in four corners. Pieces like bishops and queens can gain maximum mobility in the center. It makes sense that the center of the board is the most contested area, thus maximizing the threat to the opponent and gaining more control of the board. In contrast, the piece at the corner has the least mobility so minimizes its threat, which makes the corner position the least popular.
For white, e4 and d4 can become the most popular first move because it gives the queen and bishop mobility, thus taking and controlling the central area to gain the advantage. For d4, it needs to take an extra step to move the queen to the central area so it's less popular than e4.
When white takes e4, Black's moves are out for the same reason as white, to get the queen and/or bishop to the center. C5 might be used to limit the d4 for white's next move. If white's move is d4, d5 and Nf6 are able to stop the pawn from moving forward, and e6 can make space for the queen and bishop to move. The first turn already showed some information about the game strategy both micro and macro.
3. Algorithms applied in this study
3.1. Epsilon-greedy algorithm
In a multi-armed bandit problem, the gambler needs to face a set of slot machines and each machine will generate a random reward. The bandit algorithm here will help the gambler decide which arm to pull and how many times the arm will be pulled, thus getting an overall best reward. The main problem is the exploration-exploitation dilemma. Exploration means trying more arms and exploitation means picking the best arm in the current situation [5].
The epsilon greedy algorithm is a method to deal with this dilemma. It balances exploration and exploitation by choosing exploration and exploitation randomly. Based on the basic greedy algorithm, the algorithm will always choose the best arm in the current situation. It might generate a poor result in long term [6]. The epsilon means the probability that the algorithm will explore a new arm. If one assigns a big value to the epsilon, the convergence will be faster thus the learning speed will be faster, cause it will reach the best arm faster. Vice versa, if the epsilon is small, it will learn slower but the average reward will be higher [7].
3.2. Thompson Sampling
The idea of Thompson sampling is to pick a prior over a set of possible environments before the game start, and in each round, the learner samples an environment from the posterior and take actions based on the optimal action in that environment [8].
The exploration of Thompson Sampling is based on randomization. The posterior will affect the fluctuation in the samples. If the posterior is scattered, it is expected to be large and likely to be explored. As more data is read by the algorithm, the posterior tends to concentrate on one environment, then the exploration rate will decrease [9].
4. Experiment
The experiment first focuses on the first turn. The reward was defined from the white's perspective. For white's victory, the reward sets to 1, and the reward sets to -1 for black's victory. The reward for the draw will be set to 0. In this paper, the A/B testing is chosen as the baseline, and the author runs the A/B testing, epsilon greedy algorithm, and Thompson sampling in order. Then, all the performances of these graph are plotted and combined into Figure 5. In Figure 5, 10000 pieces of information about the opening are simulated by three algorithms. The percentage of winning by the opening move is presented on the y-axis and the number of total openings recommended to take is on the x-axis. During the experiment, the epsilon greedy used two values for epsilon. One is 0.1 and the other one is 0.02. Each algorithm iterated 10 times to find out the average.
The A/B testing shows an average performance during their testing period. It only shows improvement after the test is concluded. During its test phases, all moves were recommended by the same portion [10]. In Figure 5, the A/B testing achieved an overall good result.
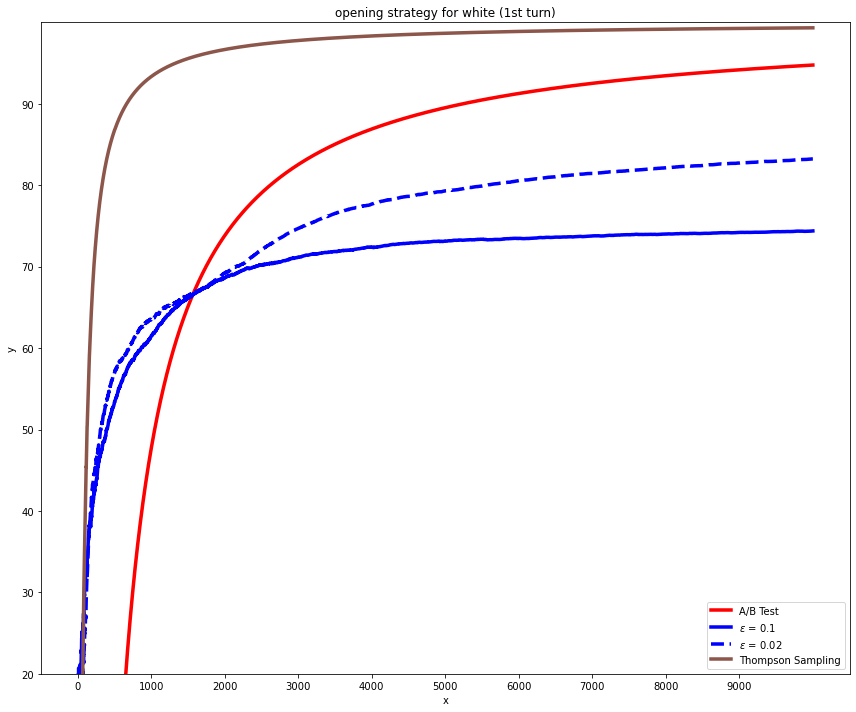
Figure 5. The learning result of the opening strategy in white’s perspective in first turn.
N-visit (test period) is set to 300.
X: number of recommended move; Y: percent of the recommended move wins
The epsilon greedy algorithm in short term is better than the A/B testing. When epsilon is equal to 0.1, it converges faster but only converges around 70%. This is because the epsilon greedy algorithm balances the exploration and exploitation through epsilon. The epsilon value decides the fraction of time the algorithm will be used on exploration, but this fraction is constant for the same bandit. When the epsilon value is set to 0.02, it will spend more time on exploration but the curve converges at a higher position which resulted in a better performance in long term.
In Figure 5, it seems that A/B testing achieved a better result than the epsilon greedy in long term even for the epsilon value set to 0.02. However, epsilon greed is still a better algorithm. The reason for this is that the test period is small. The n\_visit is set to 300 in Figure 5. When the test period sets to a larger value, 2000; in Figure 6, the performance of the epsilon greedy and Thompson sampling is not affected, but the A/B testing is hugely affected. It is obvious that epsilon greedy was way better than the A/B testing.
Thompson sampling is the best one out of all the three algorithms in both the short term and long term. It is because of its dynamic rate of exploration. It will explore more often in the beginning and explore less often through time, thus giving it high performance in both the short term and the long term.
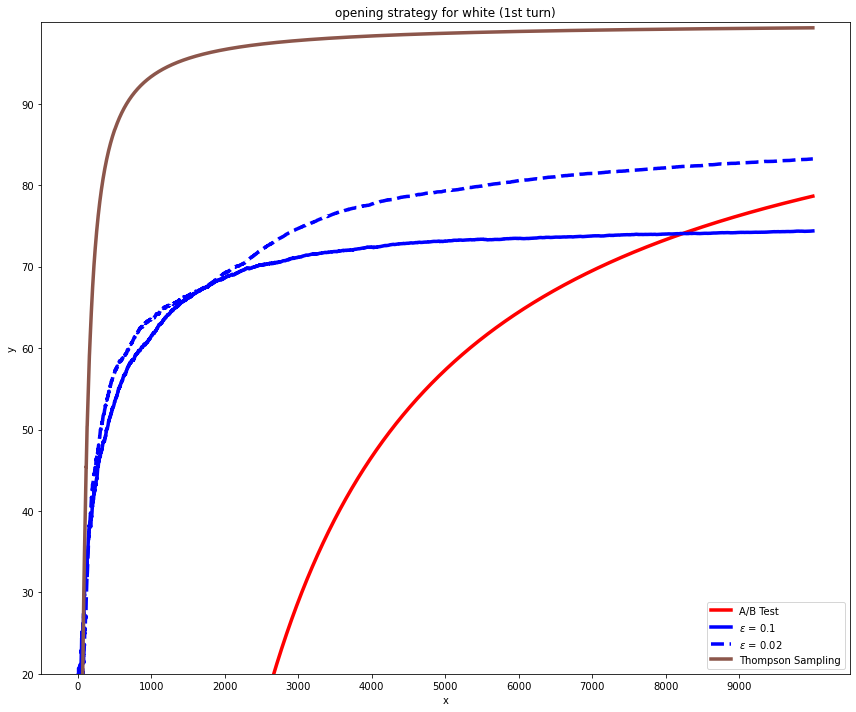
Figure 6. The learning result of the opening strategy in white’s perspective in first turn.
N-visit (test period) is set to 2000.
X: number of recommended moves; Y: percent of the recommended move wins
Since Thompson sampling has the best performance, it is chosen to analyze the result. First, the ten openings which have the highest mean reward was chosen, and I use the stack plot to plot out the graph.
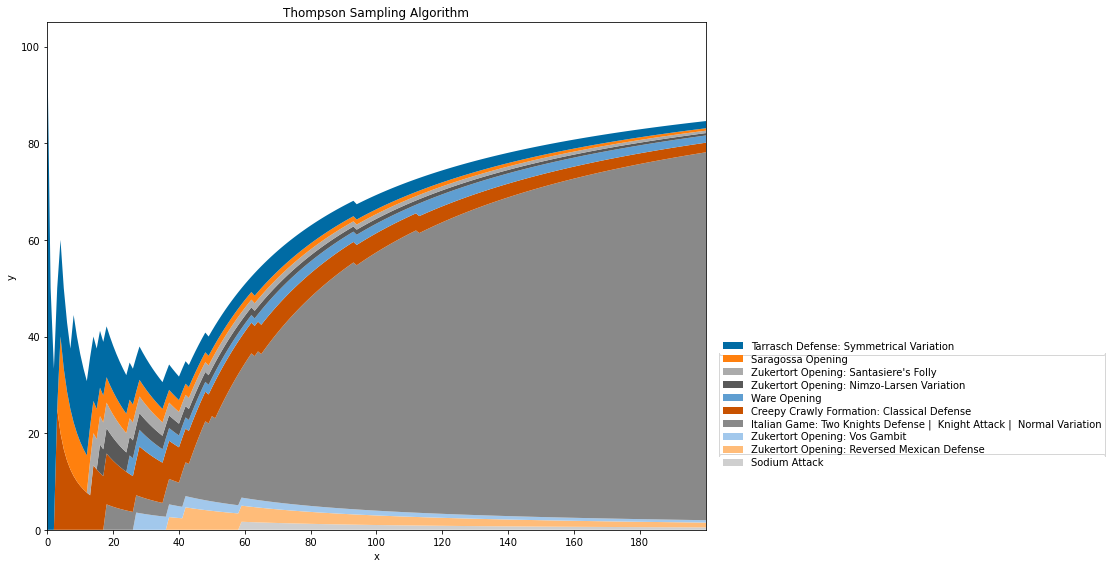
Figure 7. Thompson Sampling result of the white opening strategy.
X: number of recommended move; Y: percent of the recommended move wins
In Figure 7, it is obvious to see that the first seven openings all achieved a win rate of around 70 to 80%. The last three openings have decreasing win rate. Among all of those, Tarrasch Defense is the opening that achieves the highest win rate. The result of all the experiments showed the recommended strong opening for the white side, and showed the Thompson sampling algorithm's performance.
5. Conclusion
In conclusion, this paper uses three multi-armed bandit algorithms to analyze the opening in chess. Simulations of the chess opening move clearly demonstrated that all three algorithms can reduce regret. Among these algorithms, Thompson sampling has the best performance overall. However, based on the No Free Launch Theorem, different situations still require different algorithms. Sometimes we want the algorithm to converge faster and sometimes we want better overall results. Even A/B tests are still a good tool to use in some situations. An important consideration is that the bandits algorithm will reduce the inferior usage which takes a longer time to establish the statistical significance of their performance. So programmers need to consider the trade-off of these algorithms for different situations.
This paper also uses the Thompson sampling to find out the most recommended opening for white. This paper still has room for improvement. The reward is from the white's perspective, and it also can be done from the black's perspective by reversing the reward. The paper also only analyses the opening. A good opening might give one advantage, but it does not mean it can help you win the game easily. Besides the openings, more steps can be considered and get a more macro view of the whole game.



