1. Introduction
PID controller is the most often used control method in industrial control not only because of its simple structure and operation, but also because of its effective operation [1]. It primarily applies to systems whose fundamental linear and dynamic properties do not change over time. The traditional PID controller is highly dependent on the linearity and time-varying nature of the controlled object and cannot adapt to the requirements of the modern industrial control field for nonlinear, unstable systems with higher control accuracy requirements and intelligent automation requirements.
Presently, local and international experts have proposed a number of effective control approaches and study findings for this issue. PID control technology holds a significant place in the realm of industrial process control. The traditional PID parameter optimization method relies heavily on the artificial method of the test, the accuracy is low, the process is time-consuming, and it is difficult to adapt to the requirements of modern industrial automation production; consequently, the key to improving PID control technology is to effectively implement parameter optimization.
This study examines some of the most prominent intelligent algorithms in use today, such as fuzzy control theory, artificial neural network, and group intelligence, in order to optimize the conventional PID controller. These sophisticated algorithms can increase the transient performance and steady performance of the PID controllers' response or automatically tune the controller's parameters to decrease the need for user intervention.
This study reveals the changes and liveliness intelligent algorithms have brought to the traditional control theory and application sector. Simultaneously, we compare the various effects of the same algorithm on the PID controller, representing the future development and direction of intelligent algorithms in the field of conventional control.
2. PID controller based on fuzzy control theory
Due to lengthy nonlinear, time-varying, strong parameter coupling, random disturbance, uncertainty, and imprecise field measurements, it is challenging to develop an accurate mathematical model of a complicated controlled system using conventional control methods. To govern this complex system, fuzzy control theory incorporates fuzzy set theory, fuzzy language, and fuzzy logic.
Fuzzy control theory controls the controlled item using human understanding. Operators can control the controlled object by continuous learning and operating experience, which requires an understanding of the controlled object's characteristics, control methodologies, and performance index criteria. Fuzzy control employs human intelligence to govern a system imprecisely. Its primary objective is to provide a mathematical model of language analysis for complex systems or processes, so that operators' natural language may be converted into computer-acceptable algorithm language instantaneously.
|
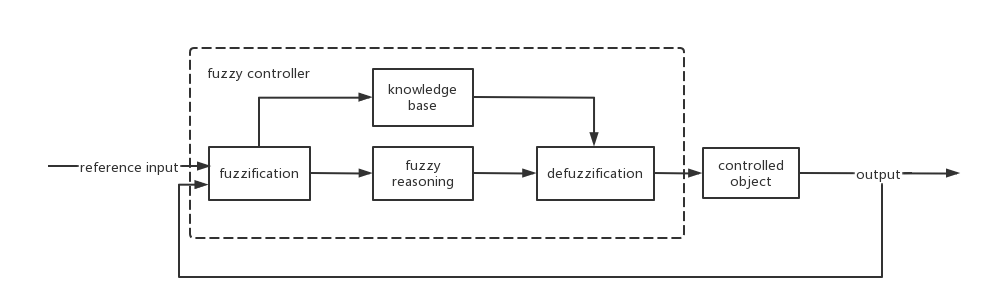
Figure 1. Block diagram of fuzzy control PID controller (original). |
The fuzzy PID controller block diagram is shown in Figure 1. In the diagram, fuzzification is the process of expressing the actual input as fuzzy sets; defuzzification is the process of outputting the exact value after the fuzzy subset after the fuzzy inference procedure is made apparent and explicit [1].
Fuzzy control design relies heavily on the knowledge base to construct the suitable fuzzy rule table based on the technical knowledge and operating experience of engineering designers [2].
The following are the steps involved in the construction of a fuzzy self-tuning PID parameter controller: It is necessary to first identify the membership function of each parameter. Both input and output variables typically have four possible values in the language: B (Big), M (Middle), S (Small), and Z (Zeros) (Zero). The curve of the membership function can then be drawn. Second, make a table of controls. Thirdly, use fuzzy reasoning and fuzzy operations. The aforementioned parameter-tweaking rule table can be expressed as a conditional statement. The parameter's argument domain is then substituted into the conditional expression to yield the parameter's value.
Nonlinear, time-varying systems with incomplete models benefit greatly from the use of a fuzzy PID controller, which has various benefits including reducing the design complexity of the system. It is a perfect example of a nonlinear controller, boasting superior robustness, fault tolerance, and response speed in the face of parameter changes. The greatest benefit of the fuzzy PID controller is the ease with which operators may utilize natural language for man-machine conversation due to the controller's model being relatively basic and not requiring the use of numerical values and language fuzzy variables to describe the system.
3. PID controller based on neural network
The self-learning and self-adaptation capabilities of the neural network operate in tandem with the tried-and-true PID control to produce a system capable of adjusting to its surroundings automatically. After the neural network PID has been calibrated, the system may respond to changes in the controlled process, make real-time adjustments to the control parameters, and enhance the control's performance and dependability. The benefits of an artificial neural network include reduced approximation error, inexpensive computation, and a simple topology, and the ability to capture nonlinear dynamics. Learning how well a system performs over time allows for optimal PID control to be implemented. To determine the parameters of the proportional unit, integral unit, and differential unit for a given optimal control law [3], a BP neural network can learn from data. Figure 2 is a schematic depicting the neural network architecture of a PID control system.
|
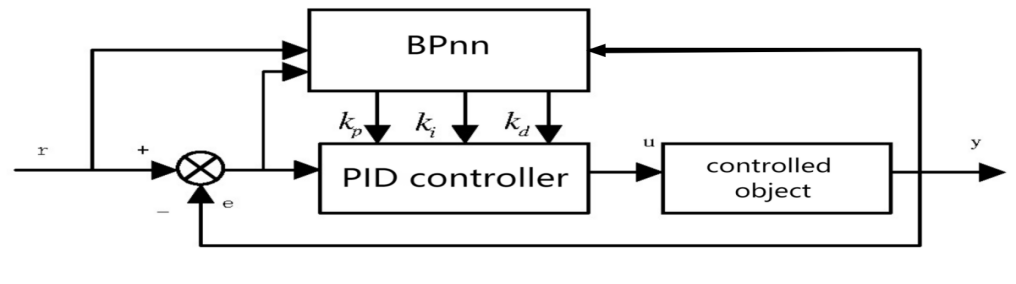
Figure 2. Structure diagram of pid control system based on BP neural network [4]. |
The most used neural network model is the BP neural network [4]. The diagram illustrates that the controller consists of two components: (1) the traditional PID controller, which is controlled and regulated by the closed-loop path; and (2) the BP neural network, which optimizes the performance of the control system and improves its ability to process complex data through adaptive learning algorithm operation of the neural network system and regulation of the series weighting coefficients [5].
A block diagram is shown where r indicates the desired value of the associated control quantity, u indicates the actual value of the corresponding control target, y indicates the output of the controlled item, and e indicates the error.
By including a BP neural network, PID can be used as an online tool for adjusting parameters. The BP neural network first iteratively learns according to the control system's data to obtain the optimal data of fitting the model, and then makes use of the adaptive ability of parameter adjustment to adjust the three parameters of PID kp, ki, and kd in real time to achieve the optimization of parameters.
A traditional PID controller's time domain expression is:
\( u(s)={k_{p}}+\frac{{k_{i}}}{s}+{k_{d}}s \)
The time domain expression for a traditional PID controller is:
\( u(t)={k_{p}}[e(t)+\frac{1}{{T_{i}}}\int _{0}^{t}e(t)dt+{T_{d}}\frac{de(t)}{dt}] \)
The corresponding discrete equation is:
\( u(k)={k_{p}}e(k)+{k_{i}}\sum _{j=0}^{k}e(j)+{k_{d}}[e(k)-e(k-1)] \)
The above function can be written as follows: kp, ki, and kd are proportions, integrals, and differentials coefficients; e(k) is just the input deviation value of the kth sampling; and u(k) is just the output value at the kth sampling time.
|
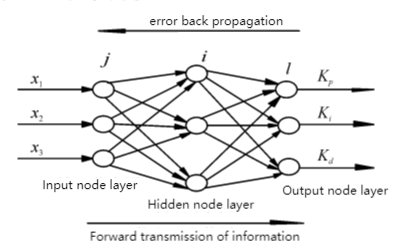
Figure 3. Neural network structure model [6]. |
In accordance with the block diagram and neural network structure model of the BP neural network, the three quantities of the input node layer of the neural network are input signal r, error e, and measured output y. Taking the structure model of the neural network as an example: the neural network is a 3-3-3 neural network, with 3 neural units in the input layer, 1 hidden layer containing 3 neural units, and 3 neurons in the output layer. The proportional gain, integral gain, and asymmetric gain of the PID controller are the output signals of the neural network.
The neural network PID controller can be paired with a swarm intelligence algorithm for further optimization. Omar et al. proposed a dynamic self-tuning neural network PID controller [7], which employs genetic algorithm to construct a database for offline training of BP neural network, ensures the data distribution in the network training database, and places the data within all operational ranges of the physical system. In addition, the particle swarm optimization technique can be used to optimize a BP neural network [8]. The next chapter discusses swarm intelligence algorithms.
4. PID controller based on swarm intelligence algorithm
Swarm intelligence is just the interaction between individuals and their surroundings. 'Swarm intelligence' refers to animal-inspired systems. Swarm intelligence algorithm is indeed a novel evolutionary computer technology. Artificial life, notably evolutionary strategy and genetic algorithm, have a special affinity with it. In recent decades, much research has been done on swarm intelligence-based optimization strategies to solve intelligent control challenges. Swarm intelligence uses genetic algorithm.
John Holland created and proposed the genetic algorithm in the US based on natural evolution. It's a computational model of biological evolution that replicates natural selection and Darwinian genetics to find the ideal answer. Combinatorial optimization, machine learning, signal processing, adaptive control, and artificial life require genetic algorithm.
|
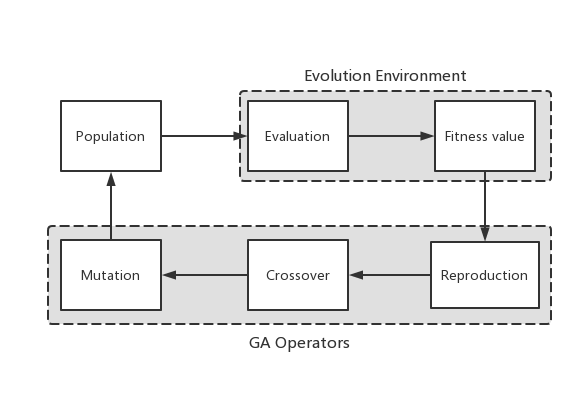
Figure 4. Genetic algorithm flow chart (original). |
The fundamental components of a genetic algorithm are encoding and decoding, an adaptation function, a selection strategy, a crossover operation, and a mutation operation. Among them, the adaptive function is the criterion for evaluating the quality of an individual; it is generally a transformation of the objective function and corresponds to the adaptability idea in biogenetics. Selection operation is the process of picking good individuals from a population based on a predetermined likelihood of change, analogous to natural selection.
Taking an ideal PID controller for electric furnace temperature based on genetic algorithm as an example [9], to precisely manage the temperature, Md. Manjurul Gani et al. presented a PID controller based on genetic algorithm in view of the long adjustment time of PID controller.
What follows is an enumeration of the various ways in which the system's overall model transfer function can be established:
\( G(s)=\frac{-0.1125s+0.15}{0.75{s^{3}}+1.825{s^{2}}+1.25s+0.2} \)
The electric furnace has a series connection to the PID controller. If the PID controller is connected in series with the rest of the system, then modifying its proportionally integrated and differential gain settings will improve the system's transient and steady-state characteristics. Since it has been determined that the parameters of variation for these features are not uniform, a genetic algorithm has been employed to determine the best possible values for the gain parameters.
Using the integral of the absolute error as the criterion:
\( IAE=\int _{0}^{∞}|e(t)|dt \)
Parameter selection of genetic algorithm and the range of Kp, Ki, Kd is shown in the following tables.
Table1. Parameters used in the algorithm [9].
Parameters | Values |
Population type | Double vector |
Fitness scaling (scaling function) | Rank |
Creation function | Constraint dependent |
Crossover | Single point |
Selection | Roulette |
Mutation | Uniform |
Population size | 20 |
Table 2. Parameter range of PID controller [9].
Parameters | Minimum values | Maximum values |
Kp | 1 | 4 |
Ki | 0 | 2 |
Kd | 3 | 7 |
First, an initial population is generated based on the selected population type, population size, and adaptability range. Next, individuals are selected using a roulette wheel selection method, an individual in the middle of the crowd is subjected to a single point variation that causes a mutation, and finally, the individual with the highest fitness, the PID parameter, is produced.
The transient response performance of the GA-PID controller to the electric furnace was greatly enhanced with a steady-state error of 0 as demonstrated by a MATLAB simulation of the step response. On the other hand, the PID controller based on genetic algorithm achieves superior results in both steady state and transient response compared to other improvement approaches as the ZN method established by Ziegler and Nichols in 1942 [10], the Cohen-Coon method, and the Nelder-Mead method [11].
5. Conclusion
This study provides a summary of the application of three common and widely employed intelligent algorithms in conjunction with PID controller, namely fuzzy control, neural network, and evolutionary algorithm, to enhance PID controller. These three methods are rather simple and have potential for development, but novices can recognize the similarities between parameter self-tuning PID controllers and comparable PID optimization concepts. Namely, they r eplace human selection and control of the three constants of a PID controller with an algorithm. PID controllers based on fuzzy theory, for instance, use human experience to determine controlling parameters; neural networks use signals from the system as input layer parameters, and their output is always the PID three parameters; the GA-PID provides a range of PID parameters and "evolves" the best individual from that range. We may also develop a PID controller based on other intelligence algorithms using this concept as a guide. If we design a PID controller based on supervised machine learning, for instance, we can input a large number of signals and artificial parameter selection results so that the machine can capture the signal's characteristics, referring to the known parameter selection method, and then output the selected parameters.
The combination of an intelligent algorithm with PID controller confers self-tuning capability on the PID controller, hence eliminating the need for manual parameter modification. In addition, the PID parameters derived from the intelligent algorithm are ideal, ensuring the precision of the findings. In addition, the intelligent algorithm-based PID controller may handle dynamic or nonlinear systems, such as boilers and other temperature control systems.
Intelligent algorithm innovation in the sphere of control goes beyond that. Not only can the algorithm be used to optimize the traditional PID, but it can also be combined with other intelligent algorithms to optimize the traditional PID. With the rising trend of artificial intelligence, the future of control will inevitably be more automated.