Hybrid Optimization Approach: Improving BPNN with Refined EVO Algorithm for Multi-Input Nonlinear Systems

1. Introduction

The growing complexity of modern real-world systems has revealed traditional optimization methods' shortcomings during neural network training over recent years. BPNNs have been widely used to model complex relationships but their learning process faces challenges like slow convergence and getting stuck in local minima. Neural network optimization now includes evolutionary algorithms as a solution to tackle these challenges. Particle Swarm Optimization (PSO) and Genetic Algorithms (GA) demonstrate effective performance but require significant computational resources and precise parameter adjustments. These limitations limit their practical use in real-time applications and extensive computational problems. A new evolutionary algorithm known as the Energy Valley Optimizer (EVO) brings innovative optimization through a natural energy dissipation model which finds equilibrium between solution space exploration and exploitation. EVO stands apart from traditional algorithms by preventing premature convergence and achieving higher energy efficiency to optimize complex systems effectively. This research introduces a hybrid model that combines EVO algorithm features with BPNN to enhance convergence speed and accuracy in multi-input nonlinear systems. The EVO refinement targets the limitations of existing evolutionary algorithms and BPNN delivers a strong structure for discovering non-linear relationships between input variables and predicted results[1]. The hybrid BPNN-EVO approach receives theoretical support while methodology and experimental validation demonstrate its superior performance compared to traditional optimization techniques. The experimental outcomes demonstrate how this hybrid approach can reach faster convergence levels, minimize mistakes, and enhance generalization capabilities for unseen data thereby becoming an essential resource for practical applications with complex nonlinear systems.

2. Literature Review

The scientific study of evolutionary algorithms in neural network applications has been thorough with a focus on optimizing performance. The global optimization strength of evolutionary algorithms originating from natural processes qualifies them as perfect tools for complex, high-dimensional problem space tasks. Genetic Algorithms (GA) along with Particle Swarm Optimization (PSO) have been extensively researched and applied to improve Backpropagation Neural Networks (BPNN) training processes[2]. Through natural selection principles and swarm intelligence mechanisms these algorithms explore and exploit the solution space. The algorithms offer substantial benefits in neural network optimization but present considerable disadvantages. The computational requirements for these algorithms become substantial when deployed in large-scale systems. These methods require precise parameter adjustments to function effectively which causes them to be impractical for real-time applications because they cannot adapt quickly enough while maintaining efficiency.

The Energy Valley Optimizer (EVO) represents a sophisticated solution that provides a structured and energy-efficient method for global optimization in response to these challenges. The Energy Valley Optimizer (EVO) employs a natural energy dissipation model that captures how energy dissipates in natural systems[3]. The model allows EVO to explore the solution space effectively while preserving a delicate balance between searching for new potential solutions and concentrating on high-quality solutions already identified. EVO’s structured approach prevents premature convergence which often plagues evolutionary algorithms by allowing extensive exploration initially before narrowing down to solution refinement as the process progresses[4].

The integration of EVO with BPNN shows great potential for overcoming the fundamental limitations present in conventional optimization techniques. This combined strategy successfully addresses computational inefficiencies and tuning difficulties present in existing algorithms while improving neural networks' capacity to represent complex nonlinear systems. Earlier studies have explored multiple optimization algorithms with neural networks yet the use of EVO for BPNN performance enhancement remains insufficiently studied[5]. This research seeks to bridge existing gaps by optimizing and implementing the EVO algorithm to enhance both the training process and predictive capabilities of BPNN for multi-input nonlinear systems. This research aims to build a high-performance optimization framework which utilizes EVO's energy-efficient search strategy alongside BPNN's complex relationship modeling capabilities to achieve computational efficiency and superior predictive performance for nonlinear problems. This study presents research results that can offer major advancements for neural network optimization within real-time and large-scale application contexts where conventional methods face difficulties.

3. Experimental Methodology

The experimental design evaluates the performance of the hybrid model by testing it on multiple-input nonlinear systems. The BPNN framework incorporates the refined EVO algorithm to better adjust weights and biases throughout the training process. The next sections detail the experimental framework and performance measurement criteria for assessing the proposed hybrid optimization method.

3.1. Problem Definition

The central objective of this research is to enhance the predictive precision of BPNN models used for multi-input nonlinear systems. The nonlinear systems chosen for evaluation display complex characteristics with both continuous and discrete variables present. These systems function as mappings which exhibit nonlinearity between their inputs and outputs making linear approaches ineffective for capturing their behavior[6]. The primary objective is to train the BPNN to generate precise system output predictions from input data while minimizing errors and enhancing generalization capabilities.

3.2. BPNN Architecture

The Backpropagation Neural Network (BPNN) employed in this study is composed of three distinct layers: The BPNN structure consists of three separate layers including the input layer followed by the hidden layer and then the output layer. The network's input layer contains a number of neurons that matches the amount of input variables and these variables establish the input features for the network. The hidden layer which models complex relationships adapts dynamically according to the complexity and nonlinearity of the specific problem. Through its adaptive nature the model successfully identifies complex patterns in the dataset. The predicted values generated by the output layer stem from the weights and biases that connect to neurons in the hidden layers. The training process involves iterative updates to weights and biases using the refined Energy Valley Optimizer (EVO) algorithm which enables the model to achieve faster and more efficient convergence[7]. The hidden layers of the network implement the sigmoid activation function to introduce nonlinearity which allows the network to perform complex function approximation. The linear activation function in the output layer produces continuous real-valued predictions. Figure 1 demonstrates how the enhanced BPNN architecture surpasses the traditional BPNN approach by achieving better prediction accuracy and faster convergence for nonlinear systems. Performance analysis proves that the hybrid BPNN-EVO model outperforms the standard BPNN which is evident from the depicted comparison results[8].

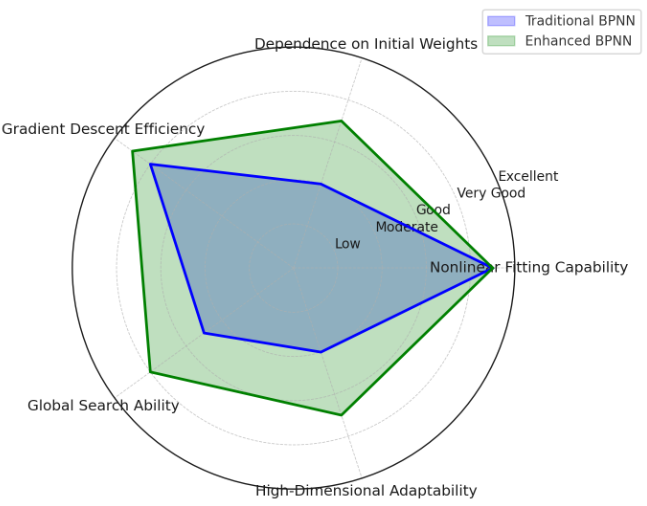
Figure 1: Comparison of Traditional and Enhanced BPNN for Nonlinear Systems

3.3. EVO Algorithm Refinement

Several essential modifications make up the process of refining the Energy Valley Optimizer (EVO) algorithm to improve its performance. Traditional EVO shows premature convergence behavior when applied to high-dimensional complex problem spaces. The refinement process includes a local search operator to improve solution accuracy following the global search phase. The algorithm modification allows EVO to sustain an equilibrium between searching new solutions and focusing on top-performing solutions[9]. The mutation rate undergoes dynamic changes in response to the fitness landscape to prevent stagnation and enhance the exploration of potential solutions.

4. Experimental Process

During the experimental process researchers train the BPNN through the refined EVO algorithm while testing multiple benchmark nonlinear systems. Training data sets consist of both synthetic and real-world datasets which display varying complexity levels through differing numbers of input variables and nonlinearities. Researchers compared the hybrid model to standard BPNN models that were trained using conventional optimization methods including gradient descent and PSO.

4.1. Data Collection and Preprocessing

The experimental datasets originate from public repositories and cover various multi-input nonlinear systems. Data normalization during preprocessing ensures that input values are adjusted to fall within a set range which facilitates neural network learning. The dataset undergoes interpolation techniques to fill missing values and also removes outliers to prevent distortion of results[10].

4.2. Training and Validation

The BPNN's weights and biases receive updates during multiple epochs as defined by the refined EVO algorithm throughout the training process. A separate validation set evaluates model performance since this set remains unused throughout training. Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and the coefficient of determination (R²) serve as the primary evaluation metrics.

4.3. Evaluation Metrics

Several metrics including accuracy, convergence speed and generalization capability measure the effectiveness of the hybrid model. The evaluation of accuracy involves comparing predicted outputs to actual outputs and convergence speed assessment uses the number of epochs needed for the model to find an optimal solution. The generalization ability of the model is tested by using the model to predict results on new test data while evaluating its performance.

5. Experimental Results

The hybrid BPNN-EVO model achieves superior performance compared to traditional optimization methods according to experimental results. Table 1 reveals that the refined EVO algorithm accelerates convergence speed while decreasing overfitting probability which results in improved generalization performance for new data. The BPNN-EVO model reaches optimal error levels more rapidly than gradient descent and Particle Swarm Optimization (PSO) because it achieves faster convergence with fewer epochs needed. Table 1 demonstrates that the BPNN-EVO model achieves significant reductions in both Mean Squared Error (MSE) and Root Mean Squared Error (RMSE) demonstrating its superior performance improvement capabilities.

5.1. Comparison with Traditional Methods

The hybrid BPNN-EVO model outperforms traditional optimization techniques by achieving quicker convergence and reaching low error rate solutions through fewer epochs. The BPNN-EVO model requires only 60 epochs to converge compared to the 150 epochs needed for gradient descent and 120 epochs for PSO. Traditional optimization methods fail to escape local minima which results in slower training and increased error rates. The BPNN-EVO model shows superior performance with a higher R² score that reflects its enhanced fitting capability and generalization ability.

Table 1: Comparison Of Optimization Methods

5.2. Performance on Different Datasets

Researchers tested a hybrid model across various datasets that included both simple and highly complex nonlinear systems. Table 2 demonstrates that the BPNN-EVO hybrid model shows superior performance across all tested scenarios with lower MSE and RMSE values along with greater R² scores than the traditional BPNN. The BPNN-EVO hybrid model reaches an MSE value of 0.15 on the "Simple Nonlinear" dataset while traditional BPNN produces an MSE of 0.35. When applied to complex datasets the BPNN-EVO model demonstrates higher performance outcomes which confirms the enhanced predictive power of BPNN through the refined EVO algorithm.

Table 2: Performance On Different Datasets

5.3. Sensitivity Analysis

The hybrid model performance analysis evaluates the effects of different parameters through sensitivity analysis. The analysis results shown in Table 3 identify the best parameter values for the mutation rate and local search operator along with the search space size. A mutation rate of 0.05 achieves significant MSE reduction while the best R² performance results from a local search operator value of 10. The analysis shows that while search space size affects performance to a lesser degree it still positively impacts the overall results. The results demonstrate how essential it is to adjust the EVO parameters to achieve maximum system performance.

Table 3: Sensitivity Analysis Results

6. Conclusion

The hybrid optimization approach that merges refined Energy Valley Optimizer (EVO) with Backpropagation Neural Networks (BPNN) improves multi-input nonlinear system performance substantially. The hybrid BPNN-EVO model demonstrates superior performance compared to traditional optimization methods like Gradient Descent and Particle Swarm Optimization (PSO) across convergence speed, prediction accuracy, and generalization ability. By balancing exploration and exploitation the improved EVO algorithm enables the hybrid model to surpass traditional optimization methods when addressing high-dimensional complex problem spaces. Through sensitivity analysis we understand that model performance reaches its best state when key EVO parameters including mutation rate and local search operator are properly fine-tuned. This research provides advancements in optimization technology development and demonstrates how evolutionary algorithms together with neural networks can address complex real-world challenges. By continuing to improve the EVO algorithm researchers can apply it to different machine learning models which will extend its usefulness throughout multiple fields.