1. Introduction
In many urban public transportation systems, adjusting the bus departure intervals according to passenger demand presents a complex and challenging problem. This challenge arises from the significant differences in passenger flows at various times and locations, especially on typical workdays, where the variations are more pronounced [1]. Although these fluctuations follow certain patterns, such as during commute peaks, they are also subject to irregular factors like weather changes and public events, making the management of public transit systems more difficult.
To effectively address this issue, scientists and engineers have been seeking flexible and intelligent solutions. This paper first provides a comprehensive analysis of existing research on optimizing bus departure intervals. By reviewing the literature, it not only understands the progress in this field but also lay a solid foundation for future work. Among the solutions, the use of PID (Proportional-Integral-Derivative) control systems for optimizing departure intervals stands out as particularly important and effective. The PID control system, a classic feedback control strategy, dynamically optimizes by collecting real-time data (such as passenger flow) during bus operations, comparing it with the preset target intervals, and making adjustments based on deviations. This not only enhances the responsiveness of public transit systems but also significantly improves passenger satisfaction and the overall efficiency of public transportation.
Through an in-depth analysis of PID control systems, this paper concludes that PID control systems, due to their reliability and efficiency, are highly valuable solutions in the field of bus departure interval optimization. They meet passengers' demands for efficient public transportation while providing transit operators with a flexible and sustainable management tool. Looking forward, as technology continues to advance, we have reason to believe that public transit systems will become even smarter and more efficient, better serving the public.
2. Systematic Literature Analysis
Li Guangchun and Nie Lei's research introduces a novel two-way cooperative algorithm for optimizing bus timetables and schedules [2]. They developed models for both one-way and coordinated two-way scheduling, integrating techniques like peak hour detection, frequency departure curves, and maximum cross-section shifts into the Bidirectional Coordination Optimization Algorithm (BCOA). BCOA synchronizes schedule adjustments with the planning process, enhancing the entire bus schedule network's efficiency. Testing on Yibin City's Bus Line 10 demonstrated its superiority over genetic algorithms, achieving five times faster solutions and a 9% reduction in trips with the same number of vehicles. It improved downstream route operating hours by 5%, addressing early operation end times and ensuring adequate rest for drivers, showcasing a highly effective approach to public transit scheduling.
According to T.W. Zhang, P.N. Huang, L. Tong, they proposed that an urban bus departure interval optimization model considering passengers' time cost is proposed [3]. Firstly, based on the detailed analysis of variables or parameters that can reflect the operating characteristics of buses, such as running speed, stopping time, the number of boarding, alighting, stranding and new waiting, we set up the constraints on vehicle operation and the number of passengers, and take the average travel time including waiting time and on-board time as the travel cost, and the average full-loading rate of the vehicles as the carrying cost of the bus company. The average travel time including waiting time and on-board time is taken as the travel cost, and the average full-load rate of the vehicle is taken as the bus company's passenger cost, and the departure interval optimization model is established with the objective of minimizing the sum of the travel cost of passengers and the passenger cost of bus companies. Then, the genetic algorithm is invoked to solve the model using the scikit-opt code base in the software Pycharm.
Based on Cao Youting’s research, she develops an optimization model for conventional bus schedules at interchange stations [4]. The optimization objective of the model is to minimize the total waiting time of passengers during the study period, and to optimize the schedule of conventional buses connecting to the urban rail transit during the study period. The waiting situation of each urban rail transit to conventional bus is categorized into three types: "happen to catch up", "just miss" and "other transfer waiting", and the perceived waiting time under different waiting types is discussed. The perceived waiting times under different waiting types are discussed and modeled. The improved selection operator genetic algorithm and the improved crossover operator genetic algorithm are designed to solve the model. According to her study, the total perceived waiting time for unevenly distributed regular buses solved by the improved selection operator genetic algorithm is 44.9% less than that of the original uniformly distributed buses, and the total perceived waiting time for unevenly distributed regular buses solved by the improved crossover operator genetic algorithm is 40.3% less than that of the original uniformly distributed buses.
According to Gong Congcong, Yang Lixing, Shi Jungang’s research, they proposed a synergistic optimization method of urban rail train schedule and train capacity allocation by considering time-varying passenger flow demand and reserved car strategy [5]. In particular, a linear integer planning model for co-optimization of urban train schedule and train capacity allocation is developed by introducing decision variables related to train departure time, number of reserved cars and passenger flow allocation scheme, with the objective of minimizing the operating cost of reserved cars and the maximum number of passengers gathering on the platform. In addition, the passenger flow allocation constraints constructed using the large M method follow the first-come-first-served principle in time and space. In order to verify the validity of the constructed model, four sets of numerical examples are set up for comparison experiments, and the optimization solver Gurobi is used to solve them. The results show that compared with the planned train schedule scheme and the two single optimization strategy schemes, the co-optimization scheme can reduce the maximum number of passenger aggregation by about 60%, 52% and 31%, and the total waiting time of passengers by about 29%, 17% and 29%, i.e., the co-optimization method can equalize the spatio-temporal distribution of urban rail train capacity and effectively reduce the risk of passenger aggregation while waiting on the platform.
The above research studies have introduced various optimization models and algorithms for bus timetables and schedules, considering factors such as passenger time cost and waiting times. Each approach has its own strengths and advantages. Li Guangchun and Nie Lei's BCOA algorithm improves the efficiency of the bus schedule network. T.W. Zhang, P.N. Huang, and L. Tong's model considers passengers' time cost and uses a genetic algorithm for optimization. Cao Youting's model optimizes bus schedules at interchange stations and reduces perceived waiting times. Gong Congcong, Yang Lixing, Shi Jungang, et al.'s synergistic optimization method effectively distributes train capacity and reduces passenger aggregation. However, Li Guangchun and Nie Lei's research on optimizing bus timetables and schedules had a limited focus on one-way scheduling and did not consider factors like peak hour detection and maximum cross-section shifts. T.W. Zhang, P.N. Huang, and L. Tong's research used a genetic algorithm for bus departure interval optimization but did not consider the coordination with the planning process. Cao Youting's research only focused on optimizing schedules at interchange stations and did not consider overall bus network efficiency. Gong Congcong, Yang Lixing, and Shi Jungang's research focused on optimizing train schedules and capacity allocation but did not consider factors like frequency and passenger comfort.
Therefore, we need the PID control system to compensate for these shortcomings and to complete the optimization of the means of departure for public transport.
3. Control system based on PID
3.1. PID Basic Theory
PID control is a common feedback control algorithm used to control engineering systems. PID controllers stabilize the output of a system near the desired value by measuring the system's error and adjusting the output according to the weights of the proportional, integral, and differential components [6]. There are three parts of the PID controller which is shown in figure 1.
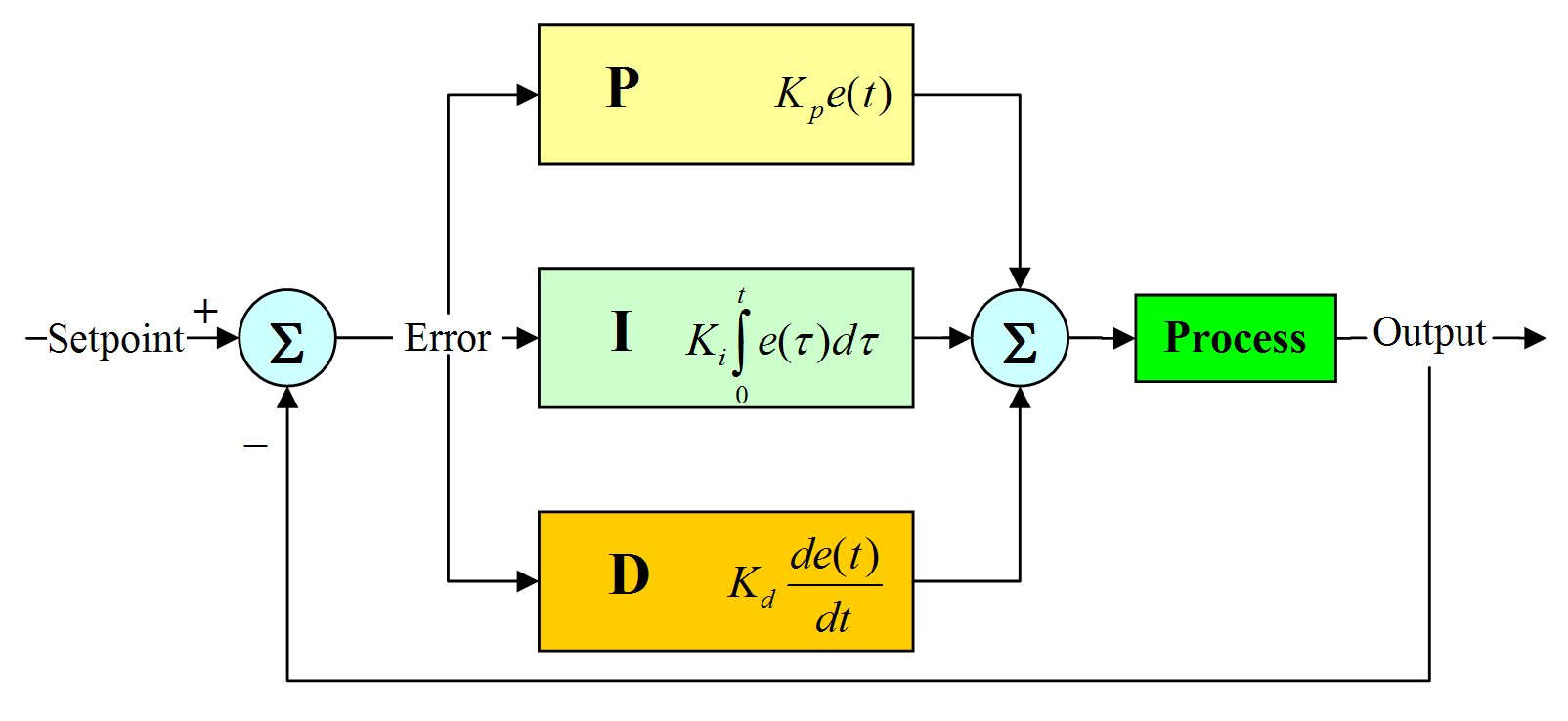
Figure 1. PID control system [6]
The first part is proportional (P) part: Proportional control adjusts the output of the controller proportionally to the magnitude of the current error in the system. The second part is integral (I) part: Integral control is used to eliminate the steady state error of the system, i.e., the long-term deviation. It controls the accumulation of error by increasing the output of the system until the error is eliminated. The third part is differential (D) Part: Differential control is used to predict the future trend of the system with respect to the error and to prevent the system from over tuning. The output of the differential controller is proportional to the rate of change of the error.
\( u(t)={K_{p}}e(t)+{K_{i}}\int e(t)dt+{K_{d}}\frac{de}{dt} \) \( (1) \)
The above formula (1) is the PID control system algorithm. Where \( u(t) \) represents the control signal output from the controller, and this signal is typically used to adjust the system to achieve the desired output; \( {K_{p}} \) represents the proportional gain, which determines the strength of the proportional part of the PID controller. The proportional part is able to provide a control action proportional to the current error; \( e(t) \) represents the control error, which is the difference between the system's current output and the desired output; \( \int e(t)d{t_{}} \) means the integral term and represents the total amount of error accumulated over time; \( {K_{i}} \) represents integral gain, which affects the magnitude of the integral term's contribution to the controller's output, and thus the system's ability to correct for long-term deviations; \( \frac{de}{dt} \) represents the rate of change of the error, that is, the rate of change over time; \( {K_{d}} \) represents differential gain, which regulates the strength of the differential term. Differential control takes into account how quickly the error changes and helps to predict the future behavior of the system, thus providing a response to rapid changes.
PID controllers have the advantage of simplicity, stability, and applicability to a wide variety of control systems. However, adjusting the PID parameters requires experience and practice to ensure the performance and stability of the control system [7]. In practice, it may also be necessary to consider nonlinear systems or to use more advanced control algorithms.
3.2. Overview of the literature review
Based on Pu Xi's research, she designed a model-free adaptive train operation tracking controller based on proportional-integral-derivative (PID) structure [8]. By adopting the model-free adaptive control to deal with the complex nonlinear system of rail transit trains, the proposed controller inherits the widely used PID structure well and avoids the conflict with the controlled object. A neural network proportional-integral-derivative (NNPID) controller is designed to cope with the problem of PID gain range and actuator limitation, and its Simulink simulation performance is better than that of other controllers.
Electric buses using the power exchange mode are developing rapidly within the public transportation sector. According to the study of Miao MIAO, LEI Xia, HE Jianping, LI Fei, the normal operation of electric bus exchange stations is related to various factors such as battery replacement and charging and grid load. In order to improve the economy of electric bus exchange station operation [9]. Firstly, we analyze and calculate the daily demand of electric buses, then we establish a dual-objective charging optimization model considering peak shaving and valley filling by minimizing the charging cost and reducing the load fluctuation, and finally, we use the weight coefficient transformation method of the genetic algorithm to solve the example. The simulation results show that the optimized charging cost can be saved by 30% and the peak shaving effect can be achieved at the same time.
In order to construct a safe and stable operation strategy for train tracking, a train tracking model was established based on the longitudinal dynamics of the train. According to the study of WANG Pengling, WANG Qingyuan, CUI Hengbin, in the model, the control objectives of train operation are different between single-car operation and multi-car operation: when single-car operation, the train runs along the curve at the optimal speed; during train tracking operation, a safe distance between trains should be ensured [10]. A hierarchical model predictive controller and quadratic optimization are applied to determine the optimal speed regulation process. Simulation was conducted based on CRH2 EMU and Wuhan-Guangzhou Railway to verify the effectiveness of the model. The results show that this method significantly improves train tracking safety and ensures ride comfort when the acceleration is -0.75~0.5 m/s2 and the jerk is -0.5~0.5 m/s3.
4. Challenges and prospects
4.1. Challenges
A control system that automatically adjusts the departure intervals of public transport vehicles aims to optimize urban traffic flow and enhance the travel experience of passengers. However, the system faces many challenges and opportunities.
First, one of the challenges lies in data processing. Accurate collection and processing of large-scale real-time data is critical to the operation of the system. Urban transportation involves complex variables such as traffic flow, pedestrian flow, and weather conditions. Therefore, the system needs to analyze these data quickly and accurately in order to adjust the departure intervals in real time.
Second, it is also a challenge to consider the traffic characteristics of different areas of the city at different times. Each urban area may have unique traffic demands, so the system needs intelligent algorithms to develop personalized departure strategies to better meet passenger needs.
In addition, ensuring stability and reliability is critical to prevent potential technical failures from adversely affecting public transportation services. Safety measures and fault tolerance within the system are key factors to ensure smooth operation of the system. As a result, higher demands are placed on system design and maintenance.
4.2. Future outlook
In terms of development prospects, the integration of IoT technology and big data analytics capabilities offers great potential for improving control systems. With the ability to utilize real-time data, these systems can achieve accurate scheduling and efficient operation. The use of smart algorithms and artificial intelligence further expands the possibilities for optimizing the system. Moreover, the integration of sustainable energy sources and the promotion of shared transportation models will create new avenues for enhancing public transportation systems. These advancements not only improve efficiency and reliability but also contribute to a more sustainable and environmentally friendly transportation network.
5. Conclusion
Undeniably, control systems that automatically adjust the departure interval of public transportation play an irreplaceable role in our daily lives. In an increasingly urbanized and congested world, these systems help optimize the movement of people and goods across busy cities efficiently and sustainably. But this is no easy feat. It requires overcoming significant data processing challenges, devising personalized departure strategies, and enhancing system stability to ensure a reliable service. With the advancements in technology and data science, we are beginning to see the emergence of a more intelligent, efficient, and sustainable public transportation departure control system. Developing such systems not only significantly improves and smoothens urban transportation but also contributes to a more liveable and greener environment for residents. By effectively managing and minimizing waiting times, optimizing routes, and fostering efficient utilization of resources, these control systems can bring about a transformational change in the way we travel, delivering a level of service that is responsive to demand and attuned to the rhythm of modern city life.



