1. Introduction
The multiplier is one of the most important parts in the process of processor design, and its running speed and efficiency directly determine the performance of the processor. In today's environment, constantly improving processor performance is needed to match the rapid development of technology, so it is necessary to carry out research related to multiplier optimization in this paper. The most important part of the design of the multiplier is to reduce the number of partial products and compress the partial product [1]. At present, the most mature optimization methods are Booth algorithm and Wallace tree structure.
In this paper, a multiplier is designed, which adopts Booth algorithm and Wallace tree structure for optimization, and inserts registers for secondary pipeline processing to further improve efficiency. Booth algorithm selects the basis 4 Booth algorithm reduces the number of partial products and avoids the problem of reduced optimization efficiency caused by circuit complexity. Wallace tree structure selects the combination of 3-2 and 4-2 compressors to compress partial products, thus reducing resource consumption and shortening critical path delay. In this paper, three optimization methods are introduced step by step. After each optimization, the current multiplier is simulated and tested, and the simulation data before the optimization is compared and analysed to confirm the optimization effect and facilitate further optimization in the future. This paper confirms the success of this design after simulation analysis, and provides some ideas and results for the current multiplier optimization field, hoping to promote the performance upgrade of the processor eventually.
2. 32 bit multiplier design and optimization principle
2.1. 32-bit multiplier design principle
The design principle of the multiplier without optimization is similar to the method of vertical expansion calculation of the base 10 column as shown in Figure 1.
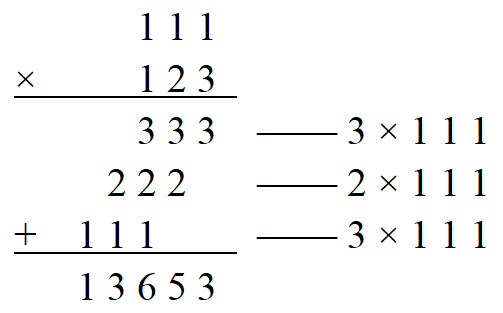
Figure 1. Vertical expansion calculation (Photo/Picture credit: Original).
The multiplicator is not processed, and the multiplier is multiplied with the multiplicator bit by bit from the lowest point, and the result obtained by each multiplication is temporarily stored as a partial product until the multiplication operation is completed with the multiplicator at the highest point, and all the partial products generated in the process are added [2]. The sum is the result of multiplication. Because this original method has great defects in time delay and expansion area, it will not be used in specific applications.
2.2. Related optimization principle of multiplier
2.2.1. Booth algorithm
Booth algorithm is used to optimize the number of non-0 partial products, and the number of non-0 partial products is effectively reduced when processing consecutive ones, thus reducing the level of the adder, and improving efficiency. The more consecutive ones, the better the optimization effect. The encoding form of the base 2Booth algorithm cannot reduce the number of generated partial products:
\( P=A×B=A×(\sum ({-x_{i}}+{x_{i-1}})×{2^{i}}) \) (1)
The encoding form of the base 4 Booth algorithm will generate part of the product number as 1/2 of the original number:
\( P=A×B=A×(\sum ({-2x_{2i+1}}+{x_{2i}}+{x_{2i-1}})×{4^{i}}) \) (2)
Therefore, it is more efficient to adopt the base 4 encoding form, and through the study of different algorithm literature, it is shown that the base 4 Booth algorithm can maintain high speed operation while maintaining low power operation in 32-bit operation [3].
The encoding form that generates fewer partial products, such as the base 8Booth encoding form, can make the number of generated partial products 1/3 of the original number. However, due to the change of the logic of generating partial products, it can no longer be realized through simple operations such as shifting, and other components need to be introduced, which makes the generating circuit of partial products complicated and reduces the optimization effect of part [4]. Therefore, it is not considered in this paper. Instead, base 4 Booth algorithm is adopted.
2.2.2. Wallace Tree
The core of the Wallace tree compression structure is the compressor, which divides the accumulation operation into multiple levels, and the full adder of each level is executed in parallel, so the delay of each level is equivalent to the delay of a full adder, and the rapid accumulation of all parts of the product can be completed with this compression structure [5].
Common are 3-2 compressors, the Carry Save Adder CSA (Carry Save Adder), and 4-2 compressors with higher compression efficiency. However, if only the 3-2 compressor module is used as the basic unit of the compression structure, the delay on the critical path will be increased, and the original design flexibility will be reduced. If only 4-2 compressor is used as the basic unit of the compression structure, it will increase the consumption of resources [6]. In order to take into account, the advantages of the two compressors, this paper adopts the tree compression structure of 3-2 compressor and 4-2 compressor.
2.2.3. Pipeline design
The basic idea of pipeline design is to divide a repeated process into several sub-processes, and then use special functional components to implement each sub-process. Because of the different components for processing each child process, the child processes that need different processing components can be executed in parallel [7]. The process is staggered in the time line, and the function components are passed in turn to achieve the purpose of improving efficiency.
The path system is divided into digital processing units (stages), and registers are inserted between each processing unit to temporarily store the data of the intermediate stages. The split units can be executed in parallel in stages without affecting each other [8]. Therefore, the pipeline design can improve the data throughput rate, that is, improve the data processing speed. As shown in Figure 2, can significantly improve the efficiency in theory.

Figure 2. Pipeline processing [8].
3. Design and optimization of 32-bit multiplier
3.1. Design of 32-bit multiplier
In binary, the cycle operation starts from the lowest part of the multiplier, traversing every bit of the selected multiplier, if the value of the multiplier is 1, then this part of the product is the multiplicator, if the value of the bit is 0, then this part of the product is all 0, every bit after the operation from the lowest part of the operation, based on the previous part of the product, and the low part of the operation is filled with 0.
After the code is expressed in this way, the main part of the multiplier design can be completed, and the declaration and definition of the required variables can be added to the beginning of the code, and the reset operation can be added to the main part and the introduction of the clock signal and the reset signal can be completed.
3.2. 32-bit multiplier optimization
In this paper, the optimization operation is carried out step by step based on 32-bit multiplier, and the optimization results are analysed and compared step by step, including Booth algorithm coding optimization, Wallace tree structure compression, pipeline processing optimization.
3.2.1. Booth algorithm optimization
Table 1 enumerates all possible value cases for \( {b_{2i+1}}{b_{2i}}{b_{2i-1}} \) , where Neg is the sign compensation bit and \( {PP_{i}} \) is the value that generates the partial product.
Table 1. Base 4 Booth encoding operation lookup table. | |||
\( {b_{2i+1}}{b_{2i}}{b_{2i-1}} \) | Neg | \( {PP_{i}} \) | Operation |
000 | 0 | +0 | Add 0 |
001 | 0 | +A | Add A |
010 | 0 | +A | Add A |
011 | 0 | +2A | Move X to the left and add |
100 | 1 | -2A | Complement X, shift to the left, add |
101 | 1 | -A | Complement X, add |
110 | 1 | -A | Complement X, add |
111 | 1 | -0 | Minus 0 |
From the above table, the corresponding part product can be obtained quickly according to the consecutive three digits of the continuous multiplier B. In binary, the *2 operation can be realized by shifting one digit to the left. The implementation method is simple and does not require additional complex circuits. The multiplier B is encoded in a base 4 Booth, and in order to be compatible with unsigned numbers, a sign bit extension of one bit is performed in the highest bit, which is 0 when operating for unsigned numbers. And give part of the product more than one bit width, to prevent the problem of overflow after the multiplier A is shifted left.
Groups in groups of 3 bits, the highest bit and the lowest bit between each of the two adjacent groups coincide, and an additional bit is added to the right of B[0], defined as B[-1], with the value 0. B[1:-1] is the first group, B[3:1] is the second group, B[5:3] is the third group, and so on, a total of 17 groups can be divided. The 17th group is not enough for 3 bits, so the highest bit is extended by a sign bit, and the extension of the sign bit will not change the value of the complement data. According to the values of each group and the search relationship in Table 3-1, corresponding partial products are obtained. A total of 17 partial products are generated, which are defined as \( {PP_{1}}-{PP_{17}} \) .
3.2.2. Wallace tree optimization
After Booth encoding optimizes the number of partial products, the accumulation process of the output 17 partial products is compressed by Wallace tree structure. If it were to use all the relatively simple and flexible 3-2 compressors in this article, this paper would need six stages of compression and one full addition [9]. In this paper considering the two level 3-2 compression after eight output value, 4-2 compressors can just completely compress, so the third level using 4-2 compressors, and produces four intermediate results, again through the level 4-2 compressors to two intermediate results, finally the use of a full adder, can get the final computation results, using the total level 4 compression level and above. The combined use of the two compressors in this paper can greatly shorten the critical path length again and improve the efficiency, as shown in Figure 3 and 4.
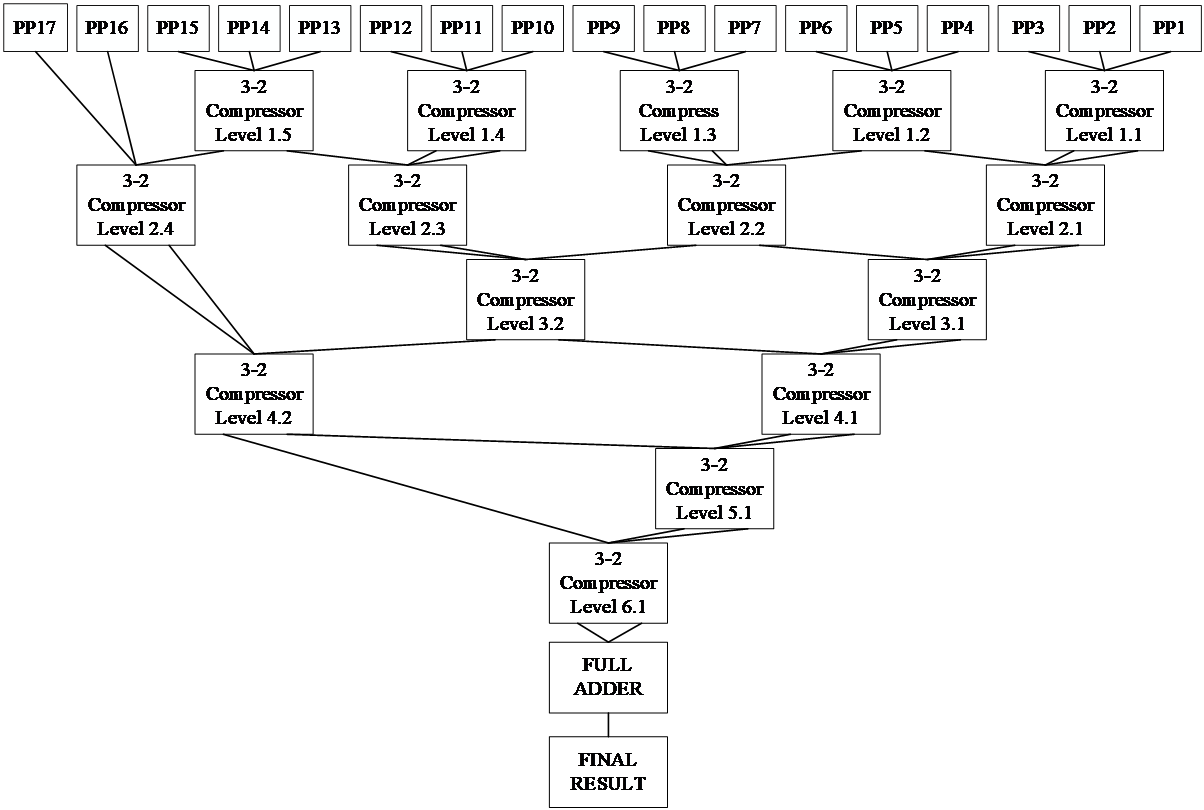
Figure 3. 3-2 compression (Photo/Picture credit: Original).
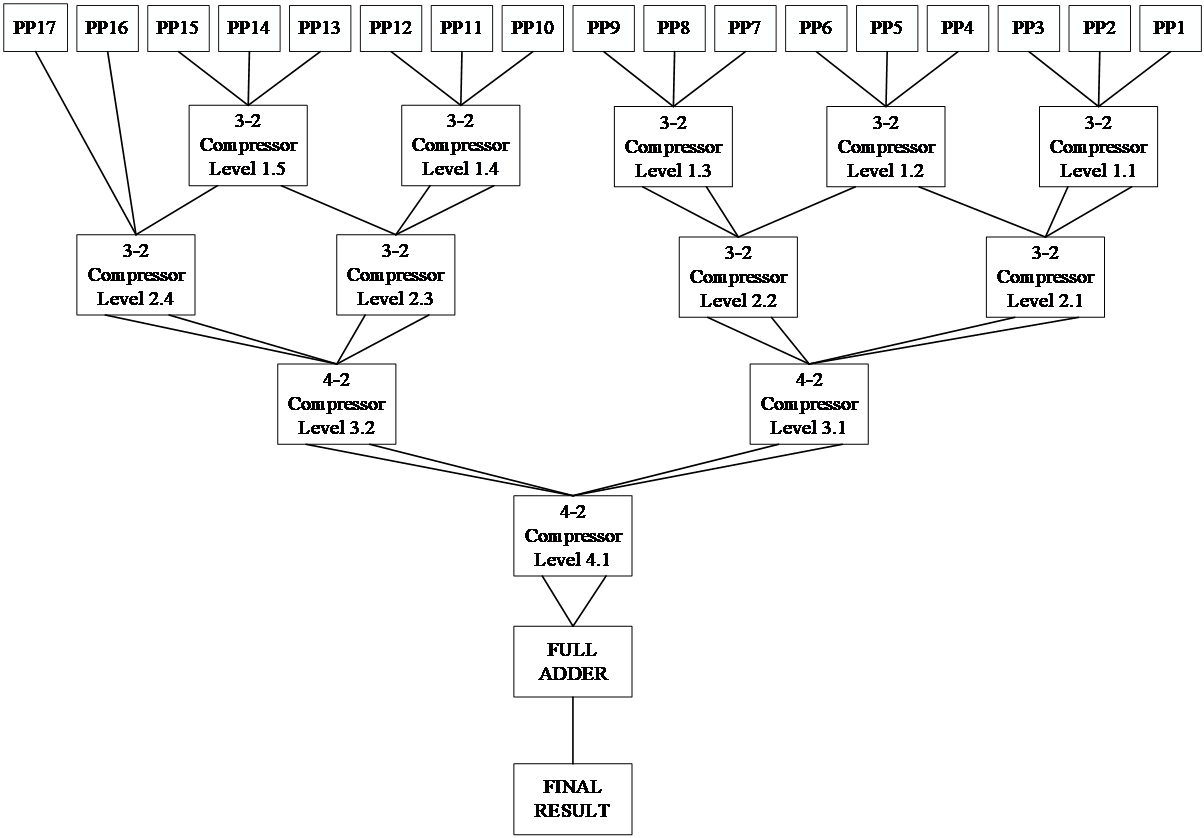
Figure 4. 4-2 compression (Photo/Picture credit: Original).
3.2.3. Pipeline design optimization
Finally, the entire multiplication operation is divided into two parts, and the intermediate state is saved with a register for pipelining, which is divided into the following two stages: The first stage: Input: two operands A and B of the multiplier, clock signal clk, enable signal en. Output: The intermediate result of a partial product. In this stage, the two operands are processed according to the Booth algorithm to produce an intermediate result of a partial product. The second stage: Input: Intermediate result from previous stage, clock signal clk, enable signal en. Output: The final product result after Wallace tree optimization. In this stage, the Wallace tree structure is used to compute multiple intermediate results in parallel to obtain the final product result [10].
4. Simulation test in Modelsim
4.1. Booth algorithm optimization simulation results
Figure 5 shows the simulation result of 3.0x1234*0x1234=0x14B5A90 waveform in the test booth algorithm. We can see that y_reg is initialized to 0x1234< < 1 = 0x2468. Then y_reg moves to the right one bit at a time to get 0x2468, 0x1234, 0x91A, After that x_minus = -x = 0xFFFFEDCC. The result is 0x14B5A90. From this, we can see that the design of booth algorithm is successful, and it is faster and more efficient than the traditional algorithm.
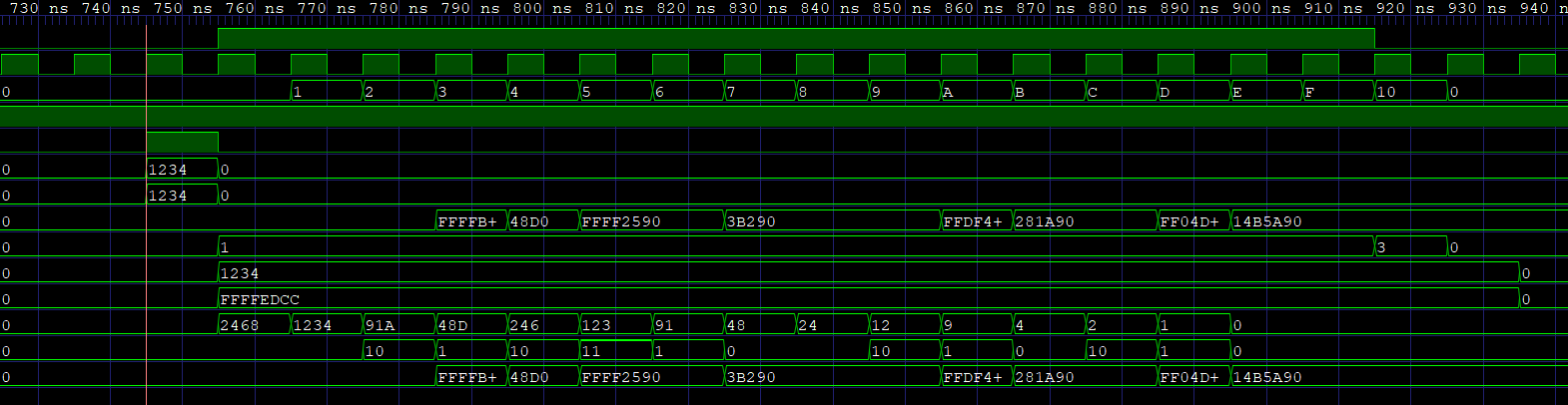
Figure 5. Simulation result of 3.0x1234*0x1234=0x14B5A90 waveform (Photo/Picture credit: Original).
4.2. Wallace tree optimization Simulation result
The main optimization of the Wallace tree is to cover the "tree" with full adder and half adder repeatedly, starting from the most data-dense place. In Figure 6, the simulation results meet expectations and are more efficient than traditional multipliers.

Figure 6. Wallace tree optimization Simulation result (Photo/Picture credit: Original).
4.3. Pipeline design optimization simulation results
Figure 7 shows the multiplier without pipelined structure and Figure 8 shows the multiplier optimized with pipelined structure.
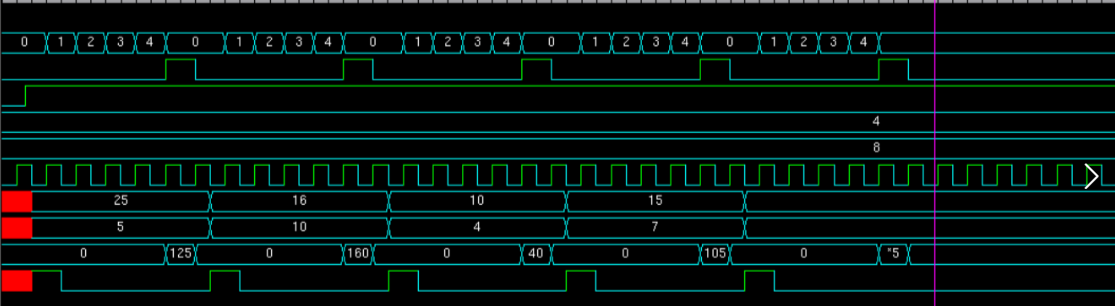
Figure 7. Multiplier without pipelined structure (Photo/Picture credit: Original).

Figure 8. Multiplier optimized with pipelined structure (Photo/Picture credit: Original).
It can obviously see that after using the pipeline structure, after a certain clock cycle, each clock cycle will output a multiplication result, and the multiplier without the pipeline structure, each result must wait for a certain clock cycle, the pipeline structure is indeed a great help to improve the computing efficiency. At the same time, pipeline structure also consumes a lot of hardware storage resources, which is a very typical design idea of using resources for efficiency.
5. Conclusion
Through this study, this paper delves into the key methods of optimizing multipliers in processor design to enhance processor performance and efficiency. By employing the optimization techniques of the Booth algorithm and Wallace tree structure, this paper effectively reduces the count of partial products and compresses the multiplication results, resulting in a significant reduction in critical path delays and resource consumption. During the optimization process, the introduction of pipeline design further boosts data throughput, achieving higher data processing speeds.
Simulation testing validates the effectiveness of each optimization step in this paper. The application of the Booth algorithm enhances the efficiency of partial product calculations, leading to faster computation speeds compared to traditional methods. The optimization of the Wallace tree structure further shortens computation paths, enhancing overall efficiency. The incorporation of pipeline design ensures that a multiplication result can be generated in each clock cycle, substantially accelerating computation speeds.
In summary, the design and optimization methods presented in this paper yield notable results in enhancing processor performance. The experimental results of this paper demonstrate that by employing the Booth algorithm, Wallace tree structure, and pipeline design, it is possible to simultaneously maintain high efficiency while effectively reducing latency and resource utilization. This provides valuable reference and guidance for further research and optimization in the field of processor design, with the potential to contribute to continuous improvements in processor performance. Through this study, the paper provides a practical and feasible solution for optimizing the application of multipliers in processor design, marking an important stride in the advancement of processor technology.
Authors Contribution
The authors contributed to this work in the following ways:
• Zeyu Zhang: Conceptualization, Investigation, Methods, Writing – Half of the Original Draft, Review & Editing.
• Bilun Wu: Data Curation, Validation, Visualization, Writing – Half of the Original Draft, Review & Editing.
All the authors contributed equally and their names were listed in alphabetical order.



