1. Introduction
The data of fresh users and new items of various internet-based applications (Taobao, Amazon shopping, Jinri Toutiao, etc.) develop swiftly with a rapid expansion of the network scale, making the issue of the recommendation algorithm more serious. Traditional recommendation algorithms speculate on the items that users have an interest in according to the previous records of users and items. However, due to insufficient historical records and features about fresh users and new items, both recommendations to fresh users and promotions of new items become hard to process. Since fresh users and new items do not receive enough feedback, a vicious cycle in which fresh users and new items are disregarded by the recommendation system can be formed.
Cold start problem is one of the common problems of the recommendation system. It refers to a circumstance in which a system or a component of it fails to function normally due to a lack of adequate data or ratings to generate valid suggestions and conclusions for users or items. In order to find a better solution to the cold start problem, this paper studies four algorithms, namely the multi-armed bandit (MAB) algorithm, the Liner Upper Confidence Bound (LinUCB) algorithm, the Collaborative Filtering Bandits (COFIBA) algorithm, and the Context-Aware clustering of Bandits (CAB) algorithm, trying to give a clear clue of the recommendation system improvement.
2. Multi-armed bandit algorithm
Recently, the MAB algorithm, as a reinforcement learning technique, has gained great popularity in the area of machine learning. The cold start issue can be successfully tackled by employing the MAB algorithm to explore the information of fresh users and new items, and then update the recommendation model online in a timely manner via user feedback.
The cold start issue is well-known and typical in recommendation systems. Because of a lack of previous data in the early stages of cold start, the recommendation system must continually investigate user information and collect user input. After the recommendation system has gathered enough information, it uses the obtained data to constantly refine the model in order to produce better suggestions. After going through the cold start phase, the MAB algorithm can obtain a good maximum total return regardless of the content value. However, in practical applications, the number of optional strategies (such as items, news, and music in the recommendation system) is often relatively large. If the content information of the strategy is not considered, the role of these algorithms is very limited.
3. Conjecture and innovation based on the multi-armed bandit algorithm
3.1. LinUCB algorithm
Confidence intervals are used by UCB to solve the Multi-armed bandit issue. A confidence interval refers to the degree of uncertainty. The larger the interval, the greater the uncertainty, and vice versa [1]. Each item's average return has a confidence interval that narrows as the quantity of trials rises (gradually deciding if the return is excellent or poor) [2]. Before every selection, the mean and confidence interval of each item are re-estimated based on the outcomes of previous tests [3], and the item with the highest confidence interval's upper limit is supposed to be chosen.
When facing a fixed number of K items (advertisements or recommended items) without having any prior knowledge, and the return of each item is completely unknown, how can the return in this selection process be maximized is a problem that can be solved by the LinUCB algorithm. It is an online learning algorithm and can handle dynamic recommendation candidate pools since features are included in the calculation. Because of the addition of features, the convergence speed is faster, and to improve computational efficiency, feature dimensionality reduction is essential.
3.2. COFIBA algorithm
In the field of advertising recommendation, the return of a choice is determined by the user and the item together, whereas the simple return of a slot machine is determined internally by the slot machine itself when the UCB algorithm adds feature information. If a feature can be used to describe the pair of the user and the item, the user will be selected before the item. The expected return and confidence interval of each arm (item) can be assessed through the feature, and the chosen returns can be generalized to various items through the feature. Building features for the user and item is an essential step in the LinUCB algorithm. The features include original user features and features of the original article [4]. Each recommended candidate item can divide the users into various groups based on their preferences. A group of users can then collectively predict the potential benefits of this item, which will have a collaborative effect. They can then observe the actual feedback in real time so as to update the personal parameters of users, which brings the concept of a bandit. In addition, it is necessary to cluster items if there are a lot of candidate items that should be recommended so that users are not grouped according to each item but rather the class cluster of each item [5]. The number of item class clusters is greatly reduced in comparison to the number of items.
The COFIBA algorithm was proposed based on these concepts, which can be summarized as follows: when the user accesses the recommendation system at time t, the recommendation system must choose the best item from the existing candidate pool to recommend to the user, observe his or her feedback, and use the observed feedback to modify the selection strategy [5]. The bandit algorithm is context-dependent because each item has an eigenvector [6]. Here, the edge relapse is as yet used to fit the client's weight vector. It is utilized to anticipate the client's conceivable criticism of everything, which is equivalent to the LinUCB calculation [4].
Compared with the LinUCB algorithm, the COFIBA algorithm is different in two aspects. For one thing, the COFIBA algorithm selects the best item on the basis of user clustering (similar to the user collective decision bandit); for another, it adjusts the clustering of user and item according to user feedback (collaborative filtering part), that is, double clustering of the user (people clustering) and the item (topic clustering), as shown in Figure 1.
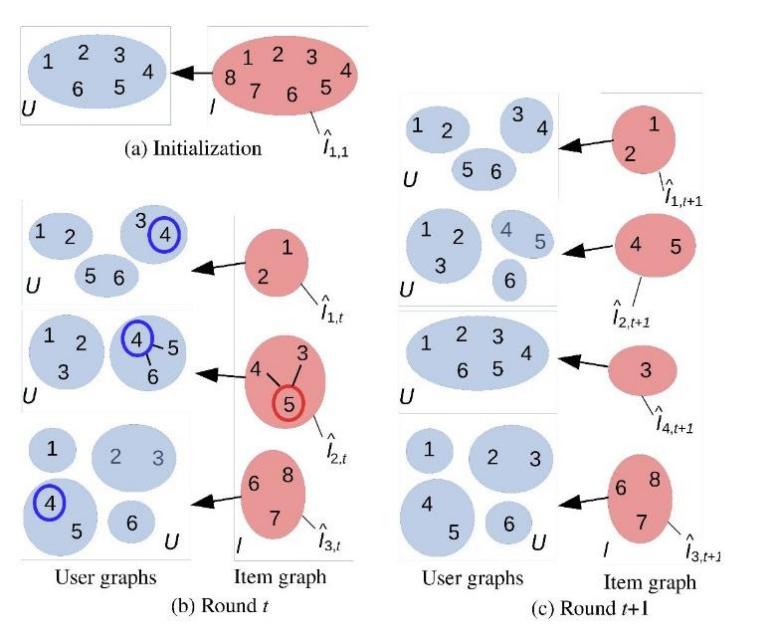
Figure 1. How to update the clustering of the user and item [7].
3.3. CAB algorithm
The CAB algorithm is a novel cluster-based algorithm for collaborative recommendation tasks. It implements a potential feedback-sharing mechanism by estimating users' neighborhoods in a context-dependent manner [8]. The CAB algorithm makes a drastic change to the current state of art models by incorporating synergistic effects into the reasoning and learning process in a way that seamlessly interweaves exploration-exploitation trade-offs and joins synergistic steps [9]. The regret bound for the data under various assumptions is demonstrated, and it exhibits a clear dependence on the number of user clusters, a natural measure of the statistical difficulty of the learning task. The prediction performance of the CAB algorithm is significantly improved on simulated and real datasets.
The process is as follows: first, processing system initialization and receiving users; then gathering the users into a certain class and calculating the cluster center: make the selection, recommend the item to the user, and receive the corresponding return; finally, updating parameters: if the confidence interval is too large, it means that the return estimate after the round of clustering and averaging the parameters is not very accurate. In this case, only user parameters should be updated.
4. Conclusion
On the basis of introducing user characteristics as content and considering the synergistic effect between users, a recommendation algorithm based on the multi-armed bandit is proposed in this paper. Combined with the analysis of the LinUCB, COFIBA, and CAB algorithms, conclusions can be drawn that the MAB algorithm gets a good maximum total revenue regardless of content value after going through the cold startup phase. In the case of large internal capacity, the CAB algorithm has the best effect.
The biggest characteristic of the LinUCB algorithm is that it optimizes the UCB algorithm. The LinUCB algorithm assumes that the return of an item is linearly related to the relevant feature after it has been selected and pushed to the user. The relevant feature refers to the context and it also occupies the most space in the actual project. As a result, the test procedure is now as follows: in order to achieve the goal of experimental learning, the characteristics of the user and the item need to be used to estimate the return and its confidence interval, the item recommendation with the largest upper bound of the confidence interval should be selected, and the parameters of the linear relationship are supposed to be updated after observing the return. Compared with the traditional UCB algorithm, the biggest improvement in the LinUCB algorithm is the addition of feature information. The interval of each candidate is no longer only estimated according to the experiment but based on the feature information.
In the field of advertising recommendation, the sample of each choice is composed of the user and the item. The user characteristics, the item characteristics, and other contextual characteristics jointly represent the choice. Using these characteristics to estimate the expected benefit of the choice and the confidence interval of the expected benefit is what the LinUCB algorithm needs to do.
The M matrix in the COFIBA algorithm is equivalent to the D matrix in the LinUCB algorithm, and both matrix dimensions are equal to the number of feature dimensions in the content space. The B vector in the COFIBA algorithm is equivalent to the C vector in the LinUCB algorithm. Improving the efficiency and stability of exploration through the prediction of a class of objects (especially when there is a large amount of data and no feedback) should be a common solution in practical applications. The COFIOBA algorithm has a better theoretical basis and accuracy [10].
The CAB algorithm makes a dramatic change to the current state of art models by incorporating synergies into the reasoning and learning process in a way that seamlessly interweaves exploration-leveraging trade-offs and adds synergistic steps. Researchers demonstrate the regret bound of the data under various assumptions, and the regret bound exhibits a clear dependence on the number of user clusters, which is a natural measure of the statistical difficulty of the learning task. Experiments on simulated and real data sets show that the predictive performance of the CAB algorithm is significantly improved compared to the most advanced methods.



