A parallel Breadth-First Search using shared memory level-synchronization

1. Introduction

The breadth-first search algorithm stands as a pivotal technique in graph traversal, systematically navigating a given graph tier by tier. Its indispensability is underscored not only in its foundational role for myriad graph-specific algorithms, like determining the maximum flow via the Ford-Fulkerson algorithm and ascertaining if a graph is bipartite, but also in its broader applications. Particularly, when data is delineated as graphs, BFS proves invaluable in tasks such as identifying relational connections within a social network or deducing the shortest route connecting two cities on a specified map [1,2]. In today's data-driven epoch, BFS's intrinsic data-intensiveness melds with the burgeoning magnitude of graph-based structures, leading to compelling challenges. The conundrum, precisely, lies in the capacity to process massive graphs efficiently, especially as transistor counts in processors reach their asymptotic limits. Hence, the imperative arises to exploit BFS in a parallelized framework, harnessing the might of multiprocessor systems. In response to this evolving need, this manuscript elucidates a level-synchronous parallel BFS technique anchored in the shared-memory paradigm. The emphasis is not merely on parallelization but also on meticulous optimizations. These refinements strategically curtail layer synchronization overheads and mitigate the intricacies tied to race conditions, ensuring the algorithm's robustness [3]. Concurrently, a discerning evaluation measures the algorithm's performance enhancements, specifically gauging the speedup in relation to the count of engaged threads.

2. Breadth-First Search

Given a graph \( G=(V, E) \) , where \( V \) is the set of vertices and \( E \) is the set of edges, and a starting vertex \( v∈G \) , BFS returns a set \( P= \lbrace v, {v_{1}},{v_{2}},…, {v_{n}}\rbrace \) such that \( ∀u∈P, u∈G \) and \( ∀{v_{i}}, {v_{j}}∈P, IsConnected({v_{i}}, {v_{j}}) \) . There are several implementations of BFS, and one classic instance utilizes a container-centric approach [4], the pseudo code shown below uses two containers called border and next_ Border, where frontier is used to keep track of all vertices at the same layer (i.e., vertices that are equally distant to the starting vertex) and next_ frontier is used to store the neighbouring vertices of those in frontier [5].

1 func serial_BFS(G = (V, E), src) {

2 levels[|V|] := a collection of level values for a given vertex v;

3 foreach vertex v in V do {

4 levels[v] := -1;

5 }

6 frontier := {}, next_frontier := {};

7 levels[src] := 0, curr_level := 0;

8 frontier.insert(src);

9 while frontier is not empty do {

10 foreach vertex v in frontier do {

11 foreach neighbor n of v do {

12 if levels[n] = -1 do {

13 next_frontier.insert(n);

14 levels[n] := curr_level + 1;

15 }

16 }

17 }

18 frontier := next_frontier;

19 next_frontier := {};

20 curr_level := curr_level + 1;

21 }

22 }

A notable characteristic of the aforementioned serial BFS implementation is its systematic exploration, wherein each layer of the graph is meticulously processed prior to advancing to the subsequent layer [6]. Such a structured approach intuitively lends itself to parallelization, especially when contemplating simultaneous traversals across individual layers of the graph. Contrarily, another prevalent BFS approach employs a queue, denoted as Q, to maintain a record of vertices awaiting exploration. Within this method, for a given vertex 'v' found in Q, vertices neighboring 'v' are sequentially appended to Q. This process is appropriately explained in the pseudocode shown below [7]. However, despite its popularity, this queuing strategy is less favored when juxtaposed with the method illustrated. The primary challenge arises in ascertaining if a specific subset of vertices genuinely coexists within an identical layer. Such a determination demands intricate dependency checks, complicating the parallelization process and thus rendering it less straightforward [8].

1 func serial_BFS(G = (V, E), src) {

2 queue := empty;

3 queue.insert(src);

4 mark src as visited;

5 while queue is not empty do {

6 v := queue.popfront();

7 foreach neighbor n : v {

8 if n is not visited do {

9 mark n as visited;

10 queue.insert(n);

11 }

12 }

13 }

14 }

3. Methodology

In the section prior, it was highlighted that the block commencing from line 10 in Figure 1 offers an avenue for parallel execution. This manuscript leans towards a shared-memory-based parallelization approach, chiefly due to its lower overhead related to communication among multiple processes, in contrast to the message-passing model [9]. To materialize this shared-memory approach, the OpenMP framework is employed, leveraging its signature fork-join model. Here, as the primary thread ventures into a parallel domain, it spawns multiple worker threads. As this parallel section concludes, these worker threads reunite with the master, ensuring a synchronized merge. Given this framework, the intuitive method for parallelization is the distribution of vertex processing duties in each layer across all accessible threads through the fork-join paradigm. However, this approach isn't devoid of challenges. Utmost vigilance is required to counter synchronization concerns emerging from race conditions. A glaring instance of such a race condition emerges in the block starting from line 12: when two threads tackle two different vertices with a mutual neighbor 'n,' the levels[n] could undergo multiple updates. To counteract this, a critical section is imperative, initially realized through the #pragma omp critical directive [10]. But there's a hitch: given that the directive locks the block rather than the data structure threads interact with, it could induce inefficiencies. These inefficiencies manifest as threads wait for another's completion. A subtler approach utilizes the #pragma omp atomic capture, targeting precise data modifications.

Furthermore, when considering vertex level values, if levels[v] remains -1 post interaction by two threads, it implies 'v' is unvisited, mandating its addition to the next frontier. This necessitates a local variable to ascertain successful level[v] updates. Another predicament is the multi-threaded addition to next_frontier, potentially skewing the BFS-intended vertex sequence. A workaround is the local_next_frontier container, recording each thread's output. On a thread's conclusion, these local vertices amalgamate into the shared next_frontier, with the merge shielded by a critical section. Finally, returning focus to parallelizing the block from line 10, a preliminary solution might be the #pragma omp parallel for directive. Yet, its implicit barrier post every loop introduces unwanted overheads. The remedy? The use of #pragma omp parallel for nowait, eliminating these barriers without synchronicity issues, thanks to the preceding atomic section introduction.

4. Results

To measure the speedup of the parallel BFS, which is defined as the ratio between the execution time taken by the serial BFS and that taken by the parallel counterpart, graph benchmarks are selected on www.networkrepository.com, and 500 experiments are run on each graph. In each experiment, the time taken by the serial BFS (in milliseconds) and the time taken by the parallel BFS (in milliseconds) are measured using omp_ get_ wtime () from <omp.h>. Upon finishing all the experiments, the average execution time for each algorithm is calculated (the average execution time is defined as the total execution time divided by the number of experiments). The experiments are run on a machine with its system specifications summarized in Table 1, and the specifications of the graphs selected for experimentation are summarized in Table 2. The speedup of the parallel BFS is plotted against the number of threads used for parallelization in Figure 1, with the maximum number of threads being 32, which is twice as many threads as there are available in the system’s processor.

Table 1. Specifications for the system used for experimentation.

Table 2. Specifications of graphs used for experimentation.

With 500 experiments run, Figure 1 plots the speedup of both graphs against the number of threads used to execute the parallel BFS.

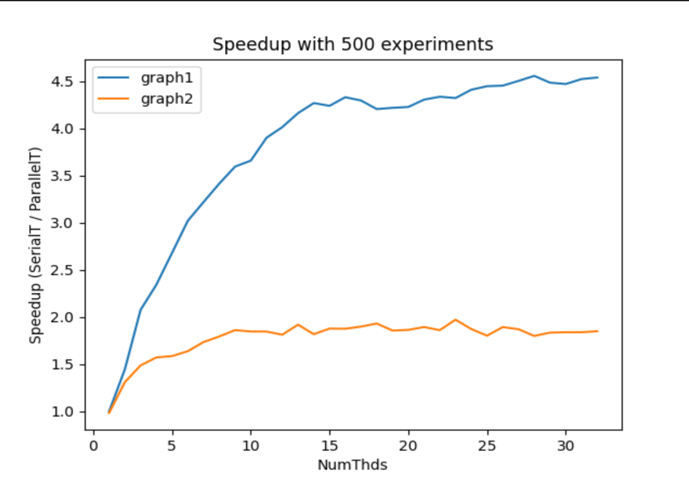
Figure 1. Speedup of the parallel BFS (Photo/Picture credit: Original).

5. Conclusions

This manuscript unveils an enhanced parallel Breadth-First Search (BFS) algorithm, meticulously designed for proficient traversal of expansive graphs on shared-memory architectures. An empirical analysis, conducted with real-world graph data sets, serves as a testament to the algorithm's robustness, exhibiting a pronounced speedup with the escalation of thread engagement. The results gleaned from these evaluations accentuate the comparative advantage of the parallel BFS over its sequential counterpart, especially when harnessing the full power of the available system threads. Statistical evaluations shed light on the performance dichotomy, offering a compelling narrative on the efficacy of both approaches. Nevertheless, future work that can lead to potentially more promising speedup as well as robustness should still be undertaken. For example, questions, such as 1) whether the directedness of a graph affects the performance of our parallel BFS implementation, 2) whether and how data partitioning that gives rise to load-balancing issues can be resolved using a shared-memory model, 3) how is the density of a graph related to the effectiveness of the parallel BFS, and 4) how scalable is the current implementation of parallel BFS, shall be investigated by controlling respective variables for reaching a quantitative conclusion.