1. Introduction
There are many types of toys designed with the goal of developing intelligence, one of the most popular puzzles is the Rubik’s Cube. It has been recognized as a symbol of challenge and entertainment. The Rubik’s Cube is a cube with 3x3 grids filled with different colours on each face. The general and most popular way of playing the cube is to change the different configuration to its original one by rotating every face of the cube. Besides that, there are also some challenging gameplays, such as “minimal steps”, “blindfolded”, “single handed”, etc. The charm and challenge of playing the Rubik’s Cube lie in the fact that there are almost infinite different configurations, the player has to observe the patterns and make decisions.
As more and more people become fascinated with this puzzle, an increasing number of competitions have been launched. Consequently, people are seeking for optimal algorithms and formulae about different configurations, just in order to reach a faster time that solves a Rubik’s Cube. As a result, the power of mathematic is applied into the development of algorithms for restoring the Rubik’s Cube [1]. In fact, the Rubik’s Cube holds a deeper significance with the knowledge of mathematic, especially of group theory – one branch of the abstract algebra, which acts cornerstone as its role in the development of the fields of mathematics. Group theory provides systematic studies in terms of symmetries and transformations, which can be linked to the Rubik’s Cube as they have similar characteristics. In fact, the vivid colors on the Rubik’s Cube can be considered as a tool for visualizing permutations [2].
Group theory studies the attributes of different groups, which consists of a set that contains elements sharing some same characteristics and an operation so that all the elements are closed under product and inversion with the operation. Since the configurations of the cube are closed (all the configurations can be obtained and restored back), the Rubik’s Cube is able to be analyzed as a group.
In fact, a group called Rubik’s Cube group has been studied, then many fantastic results are obtained. In this group, an element is a sequence of movements of the cube, so all possible configurations of it can now be represented mathematically [3]. This can lead to a better understanding of the symmetry groups. In addition, repeating a sequence of movements will always come back to its original status is a visualization of the characteristic of the cyclicity of a group. Moreover, any series rotations always yielding another state of the Rubik’s Cube is a typical example that exemplifies the closure property. Moreover, the applications of the subgroups of the Rubik’s Cube group are a type of powerful tool to explore solutions for “minimal steps” gameplay.
Therefore, the Rubik’s Cube serves as a tangible and engaging way to understand such abstract knowledges as group theory [4]. There are some published papers showing some aspects of group theory linked with the Rubik’s Cube, such as the diameter of the cube group being 20, as well as the symmetry within the Rubik’s Cube [5, 6]. This paper will explain many theories in group theory from the perspective of the Rubik’s Cube, including propositions and basic terminologies. In addition, this paper will introduce how the group theory is applied to the aspects of “minimal steps” gameplay. After all, it is hoped that this paper can show the potential of the Rubik’s Cube being a tool for visualizing the group theory, and serving as an embodiment of this abstract field.
2. Basic information of the Rubik’s cube group
2.1. Labeling the rotations
Firstly, it is necessary to briefly introduce how to play the Rubik’s Cube. Each side of it is composed by 9 coloured facets, the general goal of this toy is to rotate the faces such that each face has 9 facets with the same colour.
To represent the rotations in a convenient way, a universal method is to use several letters to represent the rotations with letters U, D, F, B, L, R, separately stands for rotating the top(upper), bottom(downward) front, back, left and right face of the cube clockwise 90°.
Particularly, if an apostrophe is on the right of a letter, that means the rotation should be anticlockwise 90° instead. Now, all the rotations can be represented by a series of letters.
2.2. Constructing the Rubik’s cube group
Since each face has 9 facets, so there are 9*6 = 54 facets in total of a Rubik’s Cube. If regard the restored status of the cube as the identity, then every configuration (the positions and orientations of all small blocks) can be deemed as obtained from the identity through a series of moves. During the movement, the 54 facets are possible to be changed their positions, so it is valid to say that the Rubik’s Cube group is a subgroup of \( {S_{54}} \) (i.e., the permutations between the numbers in the set {1, 2, …, 54}).
But is the size possible to be reduced? The answer is sure, actually it is a subgroup of \( {S_{48}} \) , because no matter how the cube is rotated or turned, the relative position of the six center facets always keep constant. Therefore, the movements of the Rubik’s Cube are the changes of the 48 remaining facets, thus concluding the result that the Rubik’s Cube group is a subgroup of \( {S_{48}} \) .
Definition 1. The symmetric group G generated by (U, D, F, B, L, R) ⊂ \( {S_{48}} \) is the Rubik’s Cube Group [7]. The operation is operated from left to right, and satisfy the law of association. The element of G represents the configuration of the Rubik’s Cube after applying the series of rotations.
Definition 2. The inverses of (U, D, F, B, L, R) are (U’, D’, F’, B’, L’, R’) correspondingly, so \( {R^{-1}} \) will be equivalent to R in the subsequent paragraphs and so on.
Example 1. The element RU \( {R^{-1}}{U^{-1}} \) is implemented by the following processes: Rotate the right face 90° clockwise, followed by rotation of the upward face 90° clockwise, then rotate the right face 90° anticlockwise, followed by rotation of the upward face 90° anticlockwise.
2.3. Aspects in group theory related to the Rubik’s cube
Group Theory has many connections to the Rubik’s Cube, the properties are obvious shown by rotating this toy and observing the related phenomena.
Firstly, as a group, G is closed under products and inversions, which are apparently true, since there are many ways to solve a specific case by different formulae. In addition, Rubik’s Cube has symmetry including rotations and reflections. The symmetric group preserves the structure of the Rubik’s Cube group under the rotation operation. Therefore, Rubik’s Cube offers a good medium to demonstrates the symmetry.
Rubik’s Cube is useful to understand cyclic group, which can be shown by repeating a series of movement, the Rubik’s Cube will always be restored. Besides, the counting of the number of cube configurations which can be done by studying the subgroup structure. Moreover, group theory creates a concept called “diameter of the Cayley graph of a group”, which effectively facilitates the development of “minimal steps” gameplay.
3. Group theory under the perspective of the Rubik’s cube
Group Theory contains many concepts and theorems, so this paragraph will introduce the concepts and theorem by definition, then provide related examples from the perspective of the Rubik’s Cube.
Definition 3. An abstract group is a set G that satisfy four axioms: (i) There is a binary operation \( * : G * G → G \) defined by \( g*h⟼gh \) , where \( gh \) represent the result of \( g*h \) , indicating the pattern of this operation. (ii) The operation is associative: \( ∀{g_{1}},{g_{2}},{g_{3}}∈G, (gh)k=g(hk) \) , which implies that operating \( gh \) first is equivalent to operating \( hk \) first. That is to say that any two elements can be operated firstly as long as there is no other element between them. (iii) There exists a unit: \( ∃e∈G, ∀g∈G:eg=ge=g. \) The element e is called the identity. (iv) Elements are invertible: \( ∀g ∈G,∃{g^{-1}}∈G. \)
These properties create a group, in which no numerical number have to be existed. Therefore, rotations of the Rubik’s Cube can definitely form a group.
Example 2. The set of all rotations of the Rubik’s Cube is a group.
Proof: For (i), the Rubik’s Cube group G is the set of all rotations of it, by the definition. So, any elements in G always give a rotation, which is definitely inside of G. The domain and range are valid. For (ii), the letters representing the rotations cannot be simplified unless they are together and they are inversed each other, then they can be cancelled. Otherwise, the letters cannot be simplified, plus the operation has an order, therefore there is no difference between the one that operate the nth, (n+1) th letters first and the one that operate the (n+1) th, (n+2) th letters first. For (iii), the restored state is the identity. For (iv), the letters’ inverses are the anticlockwise rotation of them, by the definition.
3.1. The closure property of a group
First of all, it is necessary to understand the closure property.
Proposition 1. By the definition of the abstract group, if a set \( G≠∅ \) is a group (under a binary operation), it should be closed under product and inversion.
Definition 4. A set M is closed under product if and only if \( ∀{m_{1}},{m_{2}}∈M, ∃{m^{ \prime }}∈M such that {m^{ \prime }}= {m_{1}}*m \) .
Definition 5. A set M is closed under inversion if and only if \( ∀m∈M, ∃{m^{-1}}∈M \) .
Definition 6. A subset M of a group G is a subgroup if and only if M is closed under product and inversion.
Lemma 1. A subgroup S always contain the identity element e.
Proof: Since the subgroup is closed under inversion, so \( ∀s ∈ S,∃ {s^{-1}}∈S \) . Since the subgroup is closed under product, so \( ∀{s_{1}},{s_{2}}∈S, ∃{s^{ \prime }}∈S. Let {s_{2}}=s_{1}^{-1}, \) then s \( \prime \) = e.
Example 3. The Rubik’s Cube Group is a group, so it is definitely closed under product and inversion. A detail example is that there are various ways to restore it. Suppose a configuration of the Rubik’s Cube is RUF-1BDF2RU-1 (just a randomly picked series), \( U{R^{-1}}{F^{2}}{D^{-1}}{B^{-1}}F{U^{-1}}{R^{-1}} \) is the fastest way to restore it. However, if the player uses CFOP (an effective way to restore the cube), there are dozens of steps required. Therefore, the rotations always obtain another series of rotations, it is an analogy to explain the closure property.
3.2. The symmetric group
Definition 7. Let M be a set, the set of bijections: M \( → \) M is called the symmetric group on M and denoted by Sym(M). If M = [n], it is denoted by \( {S_{n}} \) .
Example 4. Rubik’s Cube group is the a of \( {S_{48}} \) , it is implemented by labelling the 48 facets (except the center facets) with the number 1 to 48, then any rotations cause 8 edge labels and 12 corner labels to be changed. Therefore, 24 facets of the corners form a subgroup of \( {S_{24}} \) (each corner block consists of 3 faces), and the edges form a subgroup of \( {S_{24}} \) (each edge block consists of 3 faces) as well.
3.3. The cyclic group
Cyclicity is also important in group theory, the group with this property will show property that to return to the starting position, and for every cyclic group there is an order for them which describe the number of group operation.
Definition 8. A group (or a subgroup) is cyclic if and only if it is generated by a single element.
Cyclic group forms when all the elements inside this group can be obtained by repeating operating one certain element and its inverse [8].
Definition 9. Let G be a group, the minimum number n > 0 such that \( {g^{n}}=e ∀g∈G \) is called the order of the group G.
Example 5. A Rubik’s Cube can break down to three parts: edge, corner and center so do the Rubik’s Cube group G. This group can be break down into a S24 corner group and a S24 edge group (since the center will not move, there is no center group needed).
Let \( R∈G \) be a series of rotations. Let \( {g_{1}},{g_{2}} \) be the elements in the corner group and the edge group correspondingly. That is to say, \( {g_{1}} \) is the change of positions and orientation of the corner blocks, and \( {g_{2}} \) is for the edge blocks similarly.
Lemma 2. Repeating a series of rotations R can always go back to its original state.
Proof: Let the orders of \( {g_{1}},{g_{2}} \) be \( {o_{1}},{o_{2}} \) , since G is a finite group, \( {o_{1}},{o_{2}}≠ ∞ \) . Then \( {{g_{1}}^{{o_{1}}}}= {{g_{2}}^{{o_{2}}}}=e \) , let \( {o_{3}} \) = \( {o_{1}}{o_{2}} \) (it is also valid if \( {o_{3}} \) = \( {lcm(o_{1}},{o_{2}})) \) , then \( {R^{{o_{3}}}}={{g_{1}}^{{o_{1}}{o_{2}}}}{{g_{2}}^{{o_{1}}{o_{2}}}}=e \) .
This example clearly shows the cyclicity property in group theory, by concluding that repeating a series of rotations always come back to the original state, as Figure 1 shows.
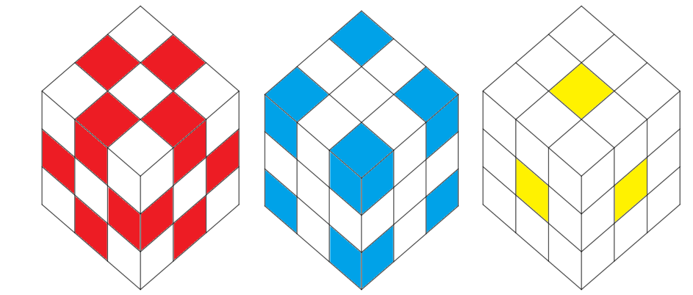
Figure 1. The different components of a Rubik’s Cube (red: edge, blue: corner, yellow: center).
3.4. Diameter of the Cayley graph of a group
Definition 10. Let G be a group and S be the set that generates G. The Cayley graph is \( the graph Γ(G,S) \) . All the vertices of this graph form a set denoted by V, and V = G. The set of edges is denoted as E, and E = \( \lbrace \lbrace g,gs\rbrace :g∈G,s∈S\rbrace \) .
That is to say, the set of vertices V is the set of all elements in the group. And the vertices are connected by the edge E which belongs to the generating set S. Any two adjacent vertices are obtained by an element and its inverse from set S each other [9]. Cayley’s graph is used for showing the relationships between each element in the group, as Figure 2 shows.

Figure 2. Demonstration of a simple Cayley’s graph.
Definition 11. Let length \( ({v_{1}},{v_{2}}) \) with \( {v_{1}},{v_{2}}∈G \) be the minimal number n satisfying \( {v_{2}}= {({s_{1}}{s_{2}}…{s_{n}})v_{1}} \) . That is to say, the minimum number of elements of S have to be applied to \( {v_{1}} \) in order to obtain \( {v_{2}} \) . The diameter diam \( (Γ) \) of the Cayley graph is defined by diam \( (Γ) \) = \( max(\lbrace length ({v_{1}},{v_{2}})\rbrace ) ∀{v_{1}},{v_{2}}∈G \) [9].
Example 6. Let the Rubik’s Cube group be G = <S>, then the diameter of the Cayley graph \( Γ(G,S) diam(Γ) \) is the maximum number n of rotations needed to obtain any configuration from any other configuration. Let the \( {v_{2}} \) be the identity e, then \( length({v_{1}},e)≤n \) . That is to say, all the configurations of a Rubik’s Cube can be restored with n steps.
In fact, the advanced research has proved that n = 20 [5]. Now 20 is known as the God’s number in this aspect [10]. It has a profound impact on the “minimal steps” gameplay which aims to find the shortest number of rotations to restore it. As a result, challengers’ spirits are encouraged as well, because some configurations were regarded as no solution less then dozens of rotations, but now they are proved with a valid solution to be found.
4. Conclusion
This paper briefly introduces the related concepts in group theory, then provides some vivid examples from the perspective of the Rubik’s Cube. Firstly, the operation of the Rubik’s Cube is introduced, followed by the construction of its group. Up to here, the basic properties of the Rubik’s Cube have been declared.
In the next part, the paragraph explains the compulsory axioms should be fulfilled if creating a group. Then, how the Rubik’s Cube fulfills those properties is explained, it gives a comprehensive understanding of those abstract concepts by using a tangible toy. After that, some knowledge in group theory is exemplified by the Rubik’s Cube. Such as closure, cyclicity, Cayley’s graph, etc.
There are related examples about the Rubik’s Cube after the definitions of those abstract concepts, so that reader can be able to understand them by just trying to rotate the Rubik’s Cube in their hands. Closure property is exemplified by rotating the toy and eventually obtain another element inside the group. Cyclicity can be studied by repeating a series of rotations, and obtain the original state as a result. Cayley graph advances the exploration of the “minimal steps” gameplay. It is worth mentioning that the vivid colors and simple structure of this toy can effectively help the learners to understand group theory quickly.
This paper is a trial that seeks to find a good way to represent the group theory, and it is successful in explaining the knowledges. This paper may inspire the teachers and learners in aspects of mathematic, to seek more tangible ways representing intangible theories, in order to enhance the understanding, as well as increasing the attractions and qualities of the presentation.
Authors Contribution
All the authors contributed equally and their names were listed in alphabetical order.



