1. Introduction
In the field of modern particle physics, subatomic particles serve as the fundamental constituents of atoms. Protons and neutrons are nestled within atomic nuclei, while electrons orbit around them. Going deeper, pro- tons and neutrons are composed of even tinier elementary particles called quarks. These quarks are held together within protons and neutrons by the strong nuclear force, which is mediated by particles called gluons.
Under conditions of extreme energy and temperature, such as those witnessed shortly after the Big Bang or recreated in high-energy particle collisions at facilities like the Large Hadron Collider (LHC), protons and neutrons can undergo a profound transformation. They can effectively disintegrate, leading to the emergence of a unique form of matter known as quark-gluon plasma (QGP). This exotic state of matter differs markedly from protons and neutrons, displaying extraordinary characteristics like extraordinarily high temperature and energy density. It exhibits collective behaviors more reminiscent of a fluid rather than individual particles, making it a subject of intensive investigation in modern physics [1-2]. In the context of ultra-relativistic collisions between atomic nuclei, the head-on collision of two nuclei leads to the production of thousands of particles, resulting in event images of remarkable complexity when compared to proton-proton collisions. The application of the Glauber model enables us to retrospectively analyze each collision, offering insights into parameters like the impact parameter, the count of participating nucleons, and the enumeration of binary nucleon-nucleon collisions [3-4].
2. Setup
2.1 We employ the nucleon data file from the Glauber Monte Carlo (MC) model, which includes information on the number of collisions and the number of partici- pants. This dataset enables us to visualize nucleon collision events, providing insights into the patterns and conditions of collisions at specific moments. This information is represented through variables such as collision count, nucleon count, and participant count.[3]
2.2 “Glauber Monte Carlo models, often referred to simply as ‘Glauber’ models, serve as valuable tools for computing geometric parameters within the initial stages of heavy ion collisions. These parameters include the im- pact parameter, the count of participating nucleons, and the initial eccentricity. In Monte Carlo-based implementations of these models, individual nucleons are randomly distributed on an event-by-event basis, and collision characteristics are determined through averaging across multiple such events.” [4]
2.3 We introduce the event planes L+ and L- as crucial components to illustrate the distribution in fine detail, leveraging the Glauber Monte Carlo model. These event planes assist our team in precisely capturing the collision region during data recording. By adjusting the orientations of L+ and L-, we can effectively sample the number of participating nucleons (Npart) from various angles. It’s worth noting that all our graphs are generated with L+ and L- set at a 90-degree angle for consistency and clarity.
2.4 Setup. We plot a scatter graph to mock the real process which is completely introduced later. Scatter graph is a proper approach to demonstrate the microscopic nucleons on computers. Thus, Monte Carlo computer simulation of the collision process has been made in two dimensions space.
We create a scatter plot as a preliminary representation for a subsequent detailed process. This scatter plot effectively mimics the microscopic behavior of nucleons within a computer simulation. The Monte Carlo simulation is conducted in a two-dimensional space to model collision events.
3. Experimental sketch and salient details
3.1. Impact parameter

Figure 1. In the context of the collision between Pb-nucleon A and Pb-nucleon B, we visualize this by considering a collision to occur when the relative transverse distance between the two nucleons is smaller than the diameter of a certain thresh- old value. We employ this graph to depict the interactions between these particles. It’s important to note that when the collision count between them is zero, we consider their inter- actions to be negligible.
3.2. Coordinate Geometry of colliding Nuclei
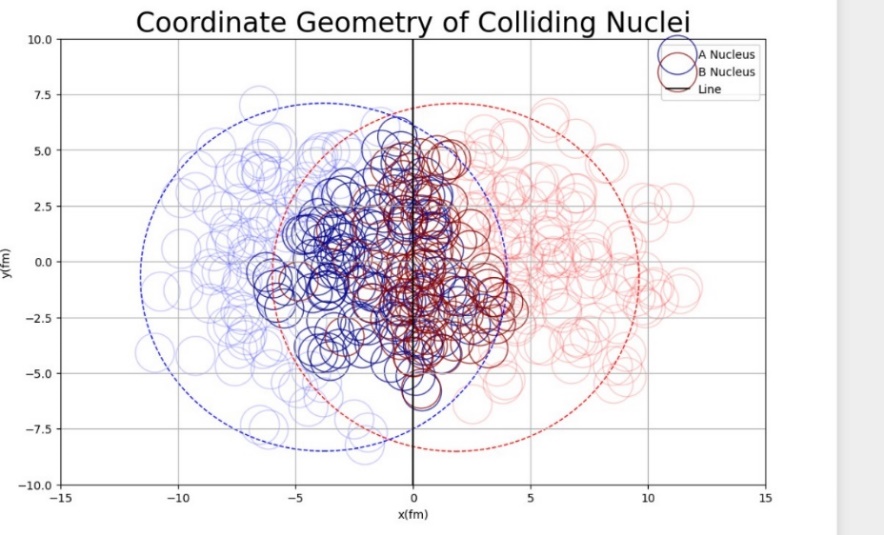
Figure 2. Create an L-axis with an initial point at (0,0) and a direction oriented at 90 degrees to form an event plane. The nucleons that engage in the collision are categorized as “participants” and are included in the cumulative count labeled “Npart.” These participant nucleons are visually distinguished with a darker color to set them apart from bystander nucleons. Conversely, bystander nucleons are those that have not yet become involved in the collision, as depicted in Figure 2.
3.3. Number of participant distribution
Therefore, when we construct a histogram of L+ versus L- and explore their association with the number of events, we observe that the most intense
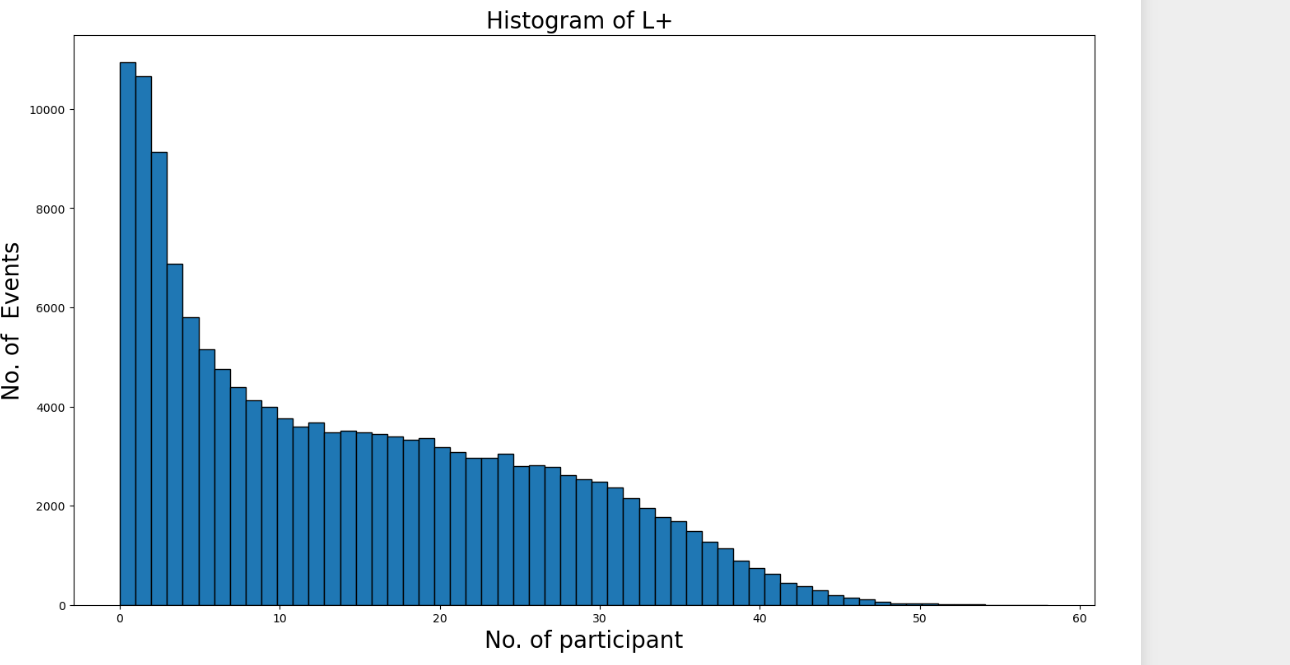
Figure 3. We are plotting a histogram depicting the number of events versus the number of participants (Npart) within the range from 0 to L+ on the x-axis. As the number of participants increases, the number of events decreases. To provide further clarity, at the beginning of the x-axis, there is a significant surplus in the number of events.
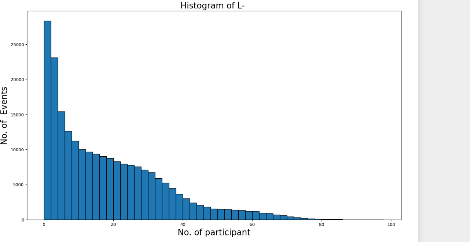
Figure 4. The No. of events descends as No. of participants increses. The histogram of No. of events vs No. of participant (Npart), from L- to 0 axis. region, indicated by the red color, is concentrated around the origin. Evidently, the distribution of participants is both centralized and symmetrical. The image illustrates a positive correlation, resembling an elliptical shape.
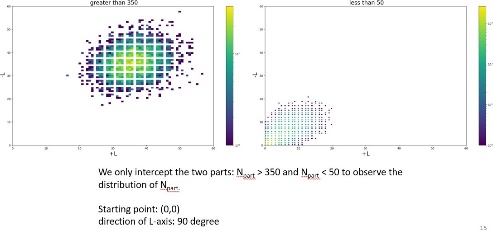
Figure 5. Certainly, two 2-D distribution images, plotting L- axis against L+ axis, were generated using Npart values: one for values exceeding 350, and another for values falling below 50.
4. Data presentation and error analysis
4.1. Nuclear densities
The nucleon density is typically described using a Fermi distribution characterized by three parameters, commonly referred to as the Wood-Saxon nucleon density.
\( ρ(r)=\frac{{ρ_{0}}(1+(ω{r^{2}})/{R^{2}})}{1+exp{((r-R)/a)}} \ \ \ (1) \)
[3], where for Pb nucleus, \( {ρ_{0}} \) represents the nucleon density at the nucleus’s center, R signifies the nu- clear radius is 6.68(fm), a denotes the skin depth is 0.54(fm), and ω quantifies deviations from a spherical shape is 0(fm).” [4-5].
4.2. Simple approach to Glauber calculations l
Consider the simple approach to Glauber calculations. In the course of a collision between two massive nuclei, particularly heavy elements like lead, occurring at ultra-relativistic speeds, a cascade of thousands of particles is produced. These lead nuclei consist of nucleons, encompassing both protons and neutrons, and the emergence of particles arises from the interactions of individual nucleons. To study these phenomena, we employed the Monte Carlo method to construct a Glauber model tailored for Pb+Pb collisions. Within this framework, we quantified crucial parameters at the femtosecond scale, including the count of participating nucleons (Npart), binary nucleon collisions (Ncoll), and the impact parameter of nucleon interactions (b).[6]
4.3. Impact parameter
In its most basic form, the Monte Carlo approach involves a nucleon-nucleon collision occurring when the distance (denoted as ‘d’) between them in the plane perpendicular to the beam axis meets the following condition: color for ease of visualization that the spectator nucleons, or the nucleons that do not participant in a collision, shown in figure beside. By revolving L+ and L-, we are able to cover Npart in different angle. In addition, our graphs are all depicted when the L+ and L- are in 90 degrees.
Commence by selecting arbitrary initial coordinates for the participant nucleons and randomly determining the directions for the L-axis. This methodology replaces the fixed origin point (0,0) for the L-axis with the randomized coordinates of a participant nucleon. Now, let’s consider the two aspects: Npart >350 and Npart < 50 to observe the distribution of Npart
We found that when we randomly select the starting point and any direction, the drawn image remains a negatively correlated function.
\( d≤\frac{\sqrt[]{σ_{inel}^{NN}}}{π} \ \ \ (2) \)
[7, 8], where σNN is the total inelastic nucleon- nucleon cross-section, d is their transverse distance.
4.4. Coordinate Geometry of colliding Nuclei and Npart
To demonstrate the distribution more detailedly, we record the collision region through L+ and L-, which are considered to be the event planesh. Any nucleon that collides is considered as a participant and is counted for an overall value designated as Npart. Each participant nucleon is colored a darker when assessing the initial state anisotropy. Our approach involved employing a simplified Glauber model to replicate nucleon collisions.
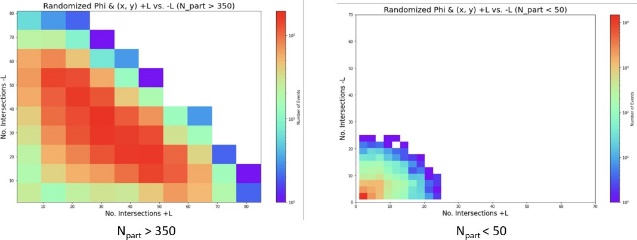
Figure 6. The No. of events descends as No. of participants increases. The histogram of No. of events vs No. of participant(Npart),from L- to 0 axis.
5. Conclusions
In this research paper, we have presented uncertainty charts generated for the Monte Carlo Glauber model The Glauber model applied in ultra-relativistic heavy- ion physics relies on nuclear geometry as its foundation. Within this framework, the concept of Ncoll is introduced, incorporating quantities that are inherently challenging to measure, such as the number of nucleons in- volved and the count of binary nucleon-nucleon collisions. Calculating the number of nucleons using the Glauber model primarily serves the purpose of facilitating com- parisons related to the observability of centrality across diverse experiments. Virtually all experiments adopt a Monte Carlo implementation of the Glauber model to calculate Npart in a consistent manner, resulting in mi- nor theoretical deviations that emerge during comparative analyses. Thus, the Glauber model operates as a theoretical framework rooted in the geometric arrangement of atomic nuclei, bridging the gap between various experimental observations and theoretical predictions.”



