1. Introduction
In the field of investment science, the term "portfolio" is used to refer to any kind of asset that an individual or institutional investor has. When confronted with a portfolio, the total expected return and the overall risk should be considered. In 1952, Markowitz published a paper entitled "Portfolio Selection," which marked the beginning of modern portfolio theory. In a single period of investment, investors respectively buy and hold a Portfolio of securities with a predetermined proportion of funds to the end of the period. Markowitz's Model tries to obtain the best point of maximizing returns and minimizing risks by optimizing the portfolio. Since Markowitz Model was published, many people have started to study it and apply it to various economic situations. Konstantinos's study examined how Markowitz Model explains risk choices [1]. In Dobre’s study, he explained how to choose a profitable portfolio by using Markowitz Model [2].
Additionally, In Theofanis, Lee, and Coralia 's study, they studied the application of the model in the Greek real estate market, Kuala Lumpur Stock Exchange, and Romanian Stock Market separately [3-5]. Zahra even uses a forecasting Markowitz model to forecast the market [6]. However, the application of the Markowitz Model in China is rarely studied.
Therefore, this study analyzes the Markowitz Model's applicability in China. In my work, I chose 20 well-known and representative Chinese stocks in the CSI 300 index and calculated their monthly returns from January 2017 to January 2022. Then I compared the returns of these 20 stocks to the market returns and performed linear regression to find the ⍺i for each period. Then I took the five best ⍺i stocks in each period, chose them as my stock picking model, and compared their returns to the market over the next cycle to see if this strategy could beat the market most of the time. If it can hit the market in most cases, then it proves that the stock selection strategy obtained by this model is excellent and then verifies the feasibility of this model in the Chinese market.
2. Theoretical Model
American economist and applied mathematician Harry Markowitz created the optimal portfolio theory for the first time. He reduced the portfolio optimization problem to a mathematical technique called quadratic optimization and introduced expected returns and standard deviation as risk measures for all the assets. The optimization problem may be stated in one of two ways: either maximize expected portfolio return while subject to constant expected portfolio risk or minimize expected portfolio risk under stable expected portfolio return. After obtaining the portfolio's Efficient Frontier curve, investors can determine the best portfolio strategy based on their preferences for risk versus return.
For the Markowitz Model, in terms of the individual stocks:
E(ri)=Rf+βim(E(rm)-Rf)+ ⍺I(1)
To be specifically,
E(ri)-Rf=βi (Rmkt-Rf)+ ⍺I(2)
3. Research
3.1. Data Collection and Processing
3.1.1. The collection of Rf, Rmkt, and Ri
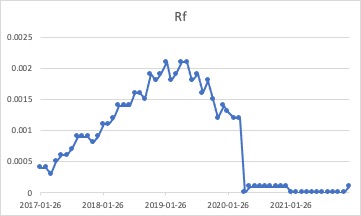
Figure 1: Rf.
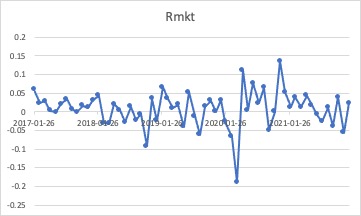
Figure 2: Rmkt.
From the Tuck Dartmouth website, I found the Fama/French Asia Pacific ex Japan 5 Factors table. In the table, I have found the risk-free return rate (Rf) and the market return rate (Rmkt). The Rf and Rmkt of China are approximately equal to that of Asia Pacific ex Japan. Therefore, I approximate these data as Chinese market data. As for Ri, I obtained the monthly yield of 20 companies from the WIND financial data terminal.
3.1.2. The Acquisition of ⍺i by Linear Regression
Using Markowitz Model, I took the market rate of return minus the risk-free rate of return (Rmkt-Rf) as X and the monthly return rate minus the risk-free rate of return (Ri-Rf) as Y. Then I performed linear regression for them. The first period is from January 2017 to January 2018, the second period is from January 2017 to April 2018, and so on, ⍺i is updated every three months.
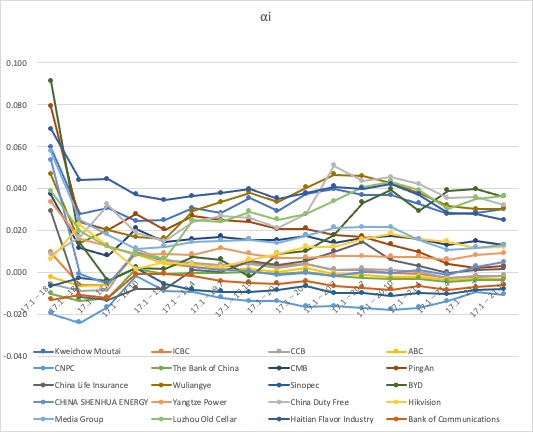
Figure 3: ⍺i.
3.1.3. The Stock Selection Strategy.
We selected the top five stocks with the highest ⍺i in each period to get the best stock selection strategy. We used these five stocks as my stock selection strategy until the next cycle (three months), and updated them in real-time.
3.2. Data Analyzing
3.2.1. The Comparison of Ri
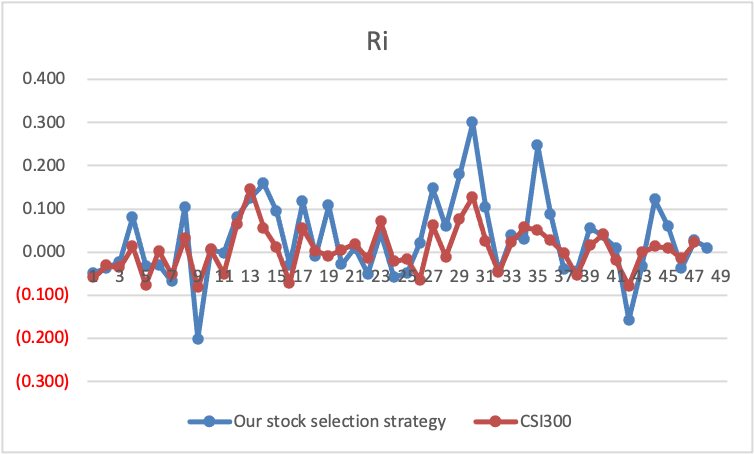

Figure 4: The selected Ri and profit.
From Figure 4, we can roughly see that the rate of return of our stock-picking strategy is slightly better than that of the market. And I also calculate the profit we can earn through this kind of stock selection strategy by using the Ri of our approach minus that of CSI 300.

Figure 5: The profit in descending order.
When we put the data in descending order, it's evident that our choice is better among 28 months out of 47 months. That is to say, compared with the market, we have won 28 times and lost out 19 times, which can prove that our stock selection strategy is effective.
3.2.2. The Analysis of the Average Rate of Profit and Stability
We can calculate that the average rate of profit is 0.025, which is a respectable yield above the market. Meanwhile, we can figure that the variance of our selection strategy is 0.009, and that of the rate of profit is 0.004. Both two conflicts are relatively small, which verifies the stability of our stock selection strategy.
There remain two special periods. The first particular period is October 2018; our stock selection strategy gave its worst performance during this period. The reason may be the international turmoil caused by the events in Syria. The second particular period is December 2020; our stock selection strategy performed best. In December, the epidemic situation in China is stable, and the country was developing steadily.
4. Conclusion
In conclusion, Markowitz's Model works well in China and can be applied to the Chinese market. The paper's initial section focuses on data processing. I have selected the Rf and Rmkt of Fama/French Asia Pacific ex Japan 5 Factors as that of the Chinese market. After obtaining the monthly data of the 20 stocks, I compute ⍺i using linear regression. Using ⍺i I selected the top 5 stocks as my stock selection strategy. Having confirmed my stock selection, I began to compare their return with the market to verify whether our selection could be better. It is concluded that our stock selection strategy is profitable and stable. Finally, we conclude that Markowitz Model can be applied to the Chinese market.
Of course, some points remain for us to explore in the future. Markowitz's Model can help us achieve profits to a great extent. However, we can continuously optimize the model to achieve greater returns and minimize risk rates [7]. Still, we can examine whether Markowitz Model suits most of the market worldwide to extend its quality and feasibility or find whether Markowitz Model has something wrong [8].



