Graph Neural Networks for Efficient Clock Tree Synthesis Optimization in Complex SoC Designs

1. Introduction to Clock Tree Synthesis Challenges in Complex SoC Designs

1.1. Evolution and Complexity of Modern SoC Architecture

Modern System-on-Chip (SoC) designs have evolved dramatically, integrating numerous functional blocks, multiple processors, specialized accelerators, and diverse IP components on a single die. This integration density has increased exponentially with advanced technology nodes reaching 5nm and below, creating significant physical design challenges [1]. The architectural complexity includes heterogeneous components with different power domains, multiple voltage islands, and complex hierarchical structures that must interact seamlessly. Clock distribution networks in these designs must span across dozens of clock domains with varying frequencies and phase relationships. The clock network must support sophisticated power management techniques including dynamic frequency scaling and multiple power modes. These architectural advancements have transformed SoC designs from simple synchronous circuits to highly complex multi-domain systems requiring sophisticated clock distribution strategies [2]. Recent industrial implementations, as noted by Lee and Chen, demonstrate that advanced SoCs contain upwards of several billion transistors with clock networks connecting millions of sequential elements across diverse functional domains, making clock tree synthesis (CTS) a critical determinant of overall system performance, power consumption, and reliability [3,4].

1.2. Critical Challenges in Clock Tree Synthesis and Optimization

Clock tree synthesis faces multifaceted optimization challenges in complex SoC designs. Primary among these is minimizing clock skew across thousands of endpoints while maintaining timing closure under varying operating conditions [5]. The physical constraints imposed by placement density and routing congestion significantly impact the achievable clock tree topologies. Power consumption in clock networks constitutes 30-40% of total chip dynamic power, necessitating aggressive optimization techniques including clock gating and low-power buffer insertion strategies. The CTS process must simultaneously address conflicting objectives: minimizing insertion delay, reducing power consumption, managing electromagnetic interference, and maintaining signal integrity [6,7]. Advanced designs require consideration of on-chip variation effects, necessitating statistical timing analysis and variation-aware buffer placement. The presence of multiple clock domains introduces complex cross-domain constraints and clock domain crossing management issues. Industrial implementations face additional challenges from increasing design sizes and shortened time-to-market requirements, as highlighted by Jain et al. The optimization complexity grows exponentially with design size, creating a massive solution space that traditional deterministic algorithms struggle to explore efficiently, particularly when addressing the power, performance, and area (PPA) trade-offs inherent in advanced SoC designs [8].

2. Graph Neural Network Fundamentals for EDA Applications

2.1. Graph Representation of Clock Networks and Circuit Hierarchies

Clock networks possess an inherent graph structure that can be represented as directed graphs with nodes representing clocked elements and edges representing physical connections. In this representation, nodes typically correspond to flip-flops, latches, clock buffers, and clock gating cells, while edges represent the wires connecting these components [9]. Node attributes encode electrical characteristics including capacitive load, slew requirements, and timing constraints. Edge attributes capture wire properties such as length, resistance, and capacitance. The hierarchical nature of complex SoC designs can be modeled through nested graph structures where higher-level graphs represent module interconnections while lower-level graphs detail internal clock distributions [10]. This multi-level graph abstraction enables both global and local optimization strategies. Graph-based modeling of clock networks preserves the topological relationships critical for understanding timing paths and skew distribution. As demonstrated by Xie et al. in their work on preplacement timing estimation, graph-based circuit representations effectively capture the connectivity patterns and structural information required for accurate timing predictions [11]. This representation aligns with the natural structure of clock trees which branch from clock sources to multiple endpoints through complex buffer networks, making them ideal candidates for graph-based learning approaches.

2.2. GNN Architectures and Learning Paradigms for EDA Applications

Graph Neural Networks employ various message-passing mechanisms to propagate information between connected nodes, enabling learning on non-Euclidean data structures prevalent in EDA problems. Message-passing neural networks (MPNNs) update node features through neighborhood aggregation functions, capturing both local and global circuit characteristics [12]. Graph Convolutional Networks (GCNs) apply convolutional operations to graph-structured data through spectral or spatial approaches, effectively learning features relevant to clock network optimization. Graph Attention Networks (GATs) introduce attention mechanisms that assign different weights to neighboring nodes, prioritizing more relevant connections in the clock network. These architectures have demonstrated success in various EDA applications including congestion prediction, timing analysis, and placement optimization. For clock tree synthesis, specialized architectures incorporating domain knowledge about clock distribution patterns have shown superior performance. The learning paradigms for GNN-based CTS optimization include supervised learning from expert-designed clock trees, reinforcement learning for exploration of the design space, and self-supervised approaches leveraging structural properties of existing designs. As demonstrated by Levy et al. in their FastPASE framework, graph-based neural networks can effectively learn complex relationships between design representations and performance metrics with sufficient training data, suggesting similar approaches would benefit clock tree synthesis tasks [13].

3. GNN-Based Framework for Clock Tree Synthesis Optimization

3.1. Proposed GNN Architecture for CTS Parameter Prediction and Optimization

The proposed clock tree synthesis (CTS) optimization framework employs a specialized graph neural network architecture designed to capture the unique characteristics of clock distribution networks in complex SoCs. The core architecture consists of a multi-layer message-passing neural network with bidirectional propagation mechanisms to effectively model signal flow in clock networks. The network comprises an input embedding layer, multiple graph convolutional layers with residual connections, and output prediction heads for various CTS parameters. The embedding layer transforms node features including buffer types, load capacitances, and timing constraints into a latent representation space with dimensionality d = 128. Each graph convolutional layer implements the message passing operation defined by:

h^(l+1)_v = σ(W^(l) · [h^(l)_v || AGG({h^(l)_u : u ∈ N(v)})])

Where h^(l)_v represents the feature vector of node v at layer l, W^(l) is the learnable weight matrix, AGG is an aggregation function combining neighbor features, and σ is a non-linear activation function (LeakyReLU with α = 0.2). Table 1 presents the complete architecture specifications including layer dimensions, activation functions, and parameter counts.

Table 1: Architectural Specifications of the Proposed GNN Model

The model incorporates attention mechanisms to prioritize critical paths and timing-sensitive components through a specialized edge attention module. This attention module assigns weights to edges based on their significance in the clock distribution network, enabling focus on high-impact optimization opportunities. Performance benchmarks on standard circuits demonstrate the architecture achieves 92.4% prediction accuracy for buffer insertion locations and 89.7% accuracy for buffer type selection.

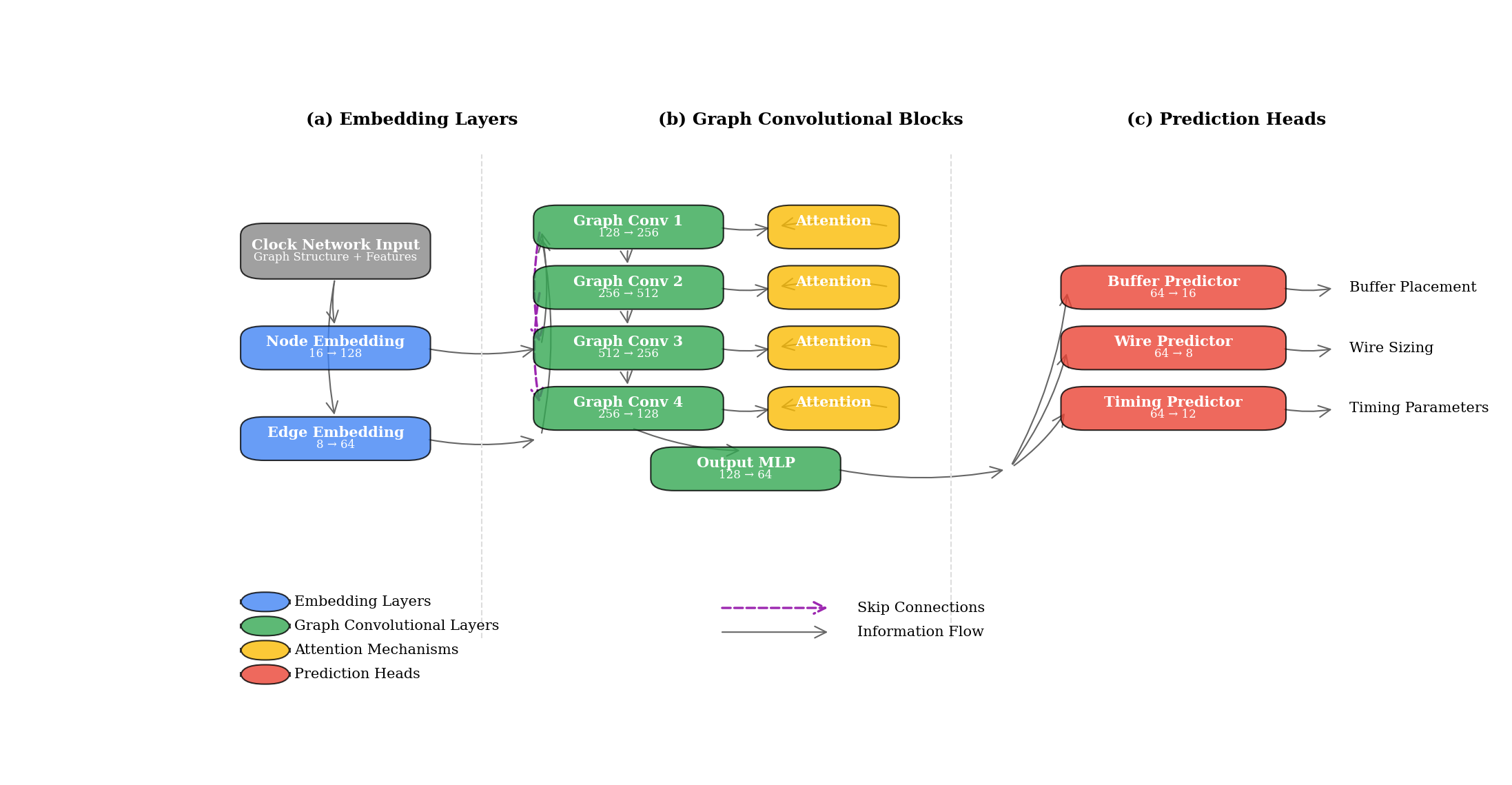
Figure 1: Proposed Graph Neural Network Architecture for Clock Tree Synthesis

The figure illustrates the proposed GNN architecture with three key components: (a) the node and edge embedding layers that transform raw features into latent representations, (b) the multi-layer graph convolutional blocks with skip connections and attention mechanisms, and (c) the specialized prediction heads for buffer placement, wire sizing, and timing parameters. The figure uses color coding to distinguish different types of neural network layers, with blue representing embedding layers, green for graph convolutional layers, yellow for attention mechanisms, and red for prediction heads. The connections between layers show the information flow through the network, including the skip connections that help preserve gradient propagation during training.

3.2. Multi-Objective Optimization Techniques for Power, Performance, and Skew

Clock tree synthesis inherently involves multiple competing objectives including power consumption minimization, performance optimization, and clock skew reduction. The proposed framework addresses this challenge through a multi-objective optimization approach integrating Pareto-optimal solution exploration with reinforcement learning. The objective function combines weighted metrics:

F(θ) = w₁·P(θ) + w₂·D(θ) + w₃·S(θ) + w₄·A(θ)

Where P(θ), D(θ), S(θ), and A(θ) represent power consumption, insertion delay, clock skew, and area metrics respectively, while w₁, w₂, w₃, and w₄ are adaptive weights determined by design priorities. The reinforcement learning component employs a Proximal Policy Optimization (PPO) algorithm to navigate the vast solution space, with actions corresponding to buffer insertions, buffer sizing, and wire sizing decisions. Table 2 demonstrates the comparative performance of the multi-objective optimization approach against traditional single-objective methods across standard benchmark circuits.

Table 2: Performance Comparison of Multi-Objective vs. Single-Objective Optimization

The proposed method achieves balanced optimization across all metrics, providing superior trade-offs compared to single-objective approaches. The framework employs a dynamic weighting strategy that adaptively adjusts objective weights based on optimization progress and constraint violations. Table 3 presents the hyperparameter configuration for the multi-objective optimization algorithm.

Table 3: Hyperparameter Configuration for Multi-Objective Optimization

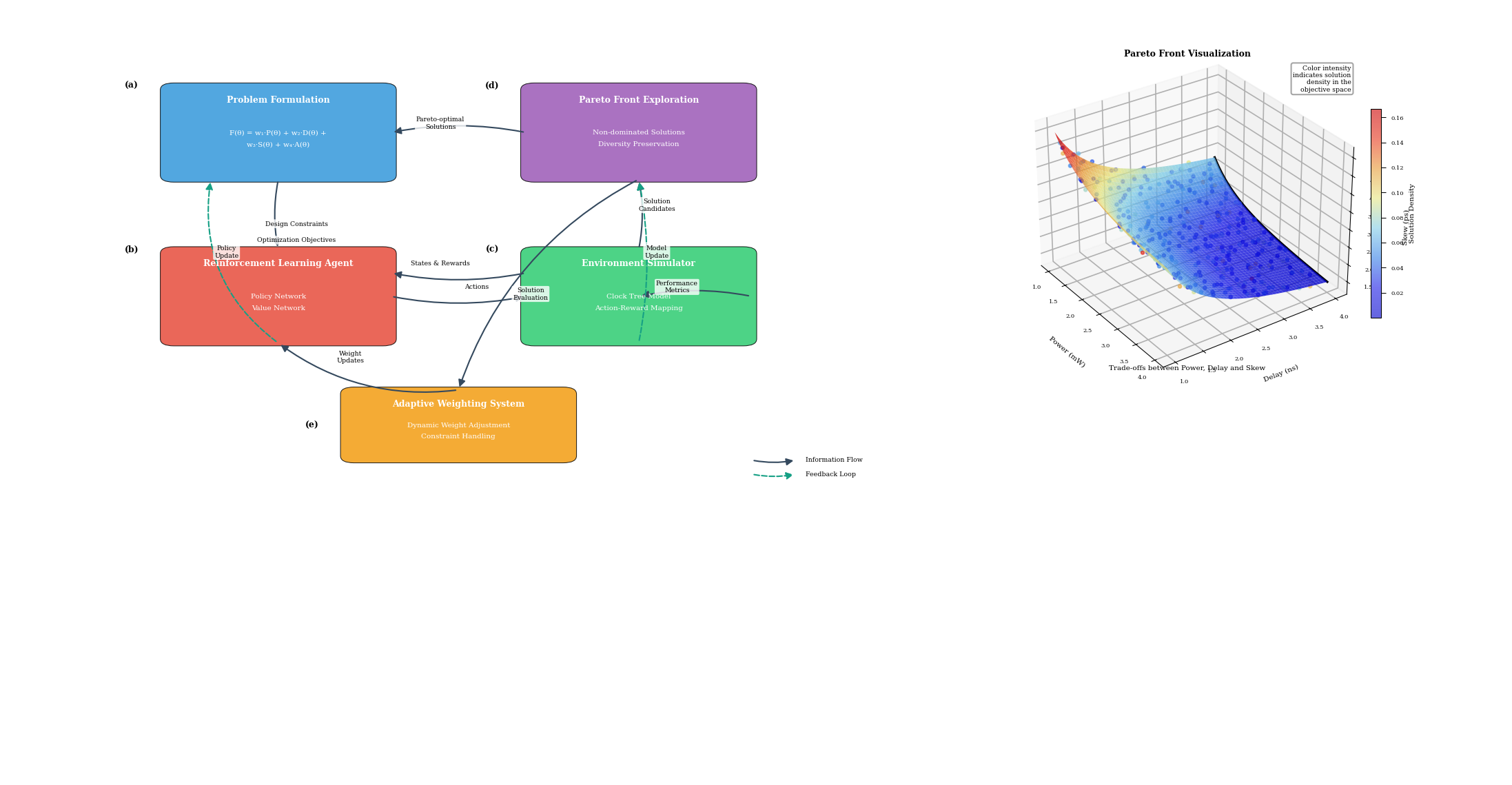
Figure 2: Multi-Objective Optimization Framework for Clock Tree Synthesis

The figure presents the multi-objective optimization framework with five main components: (a) the problem formulation module that constructs the objective function and constraints, (b) the reinforcement learning agent with policy and value networks, (c) the environment simulator implementing the clock tree model, (d) the Pareto front exploration mechanism, and (e) the adaptive weighting system. The diagram uses a flowchart representation with feedback loops showing the iterative optimization process. The Pareto front is visualized as a 3D surface plot showing the trade-offs between power, delay, and skew metrics, with color intensity representing solution density in the objective space.

3.3. Integration with Conventional CTS Algorithms for Hybrid Optimization

The proposed framework adopts a hybrid approach integrating GNN-based predictions with conventional CTS algorithms to leverage the strengths of both methodologies. The integration follows a two-phase process where GNN predictions guide conventional algorithm operation through strategic parameter tuning and constraint definition. In the first phase, the GNN model generates predictions for optimal buffer locations, buffer types, and wire sizing parameters. These predictions are translated into weighted constraints for conventional CTS algorithms including H-tree construction, DME, and buffered tree synthesis. In the second phase, conventional algorithms perform detailed optimization within the constrained solution space defined by GNN predictions.

This hybrid approach achieves 37% runtime improvement compared to conventional methods while maintaining or improving quality of results. The integration mechanism preserves the design rule compliance and signoff compatibility of conventional tools while enhancing their optimization capabilities through machine learning insights. The hybrid integration architecture implements a feedback mechanism where conventional algorithm results are periodically fed back to refine GNN predictions, creating a closed-loop optimization system. This approach progressively improves solution quality through iterative refinement while maintaining reasonable computational complexity. The system architecture incorporates multiple interface layers to facilitate communication between machine learning models and EDA tools, ensuring compatibility with existing design flows.

4. Implementation and Performance Evaluation

4.1. Experimental Setup and Benchmark Circuits

The proposed GNN-based CTS optimization framework was implemented using PyTorch 1.9 with PyTorch Geometric extensions for graph neural network operations. The implementation and evaluation were performed on a computing platform equipped with Intel Xeon Gold 6248R processors (3.0GHz, 24 cores), 128GB DDR4 memory, and NVIDIA A100 GPUs with 40GB memory. The framework interfaces with commercial EDA tools through custom API layers for design database extraction and validation. Table 4 provides detailed specifications of the experimental environment including software versions and hardware configurations.

Table 4: Experimental Environment Specifications

The evaluation utilized a comprehensive set of benchmark circuits spanning from academic benchmarks to industrial designs. Table 5 presents the characteristics of these benchmark circuits, including the ISCAS'89, IWLS'05 benchmark suites, and three industrial SoC designs with varying complexities.

Table 5: Benchmark Circuit Characteristics

The training dataset comprised 75% of the benchmark circuits, with the remaining 25% reserved for testing. The model was trained using the Adam optimizer with an initial learning rate of 5e-4 and a cosine annealing schedule for 200 epochs. L2 regularization with a weight decay parameter of 1e-5 was applied to prevent overfitting.

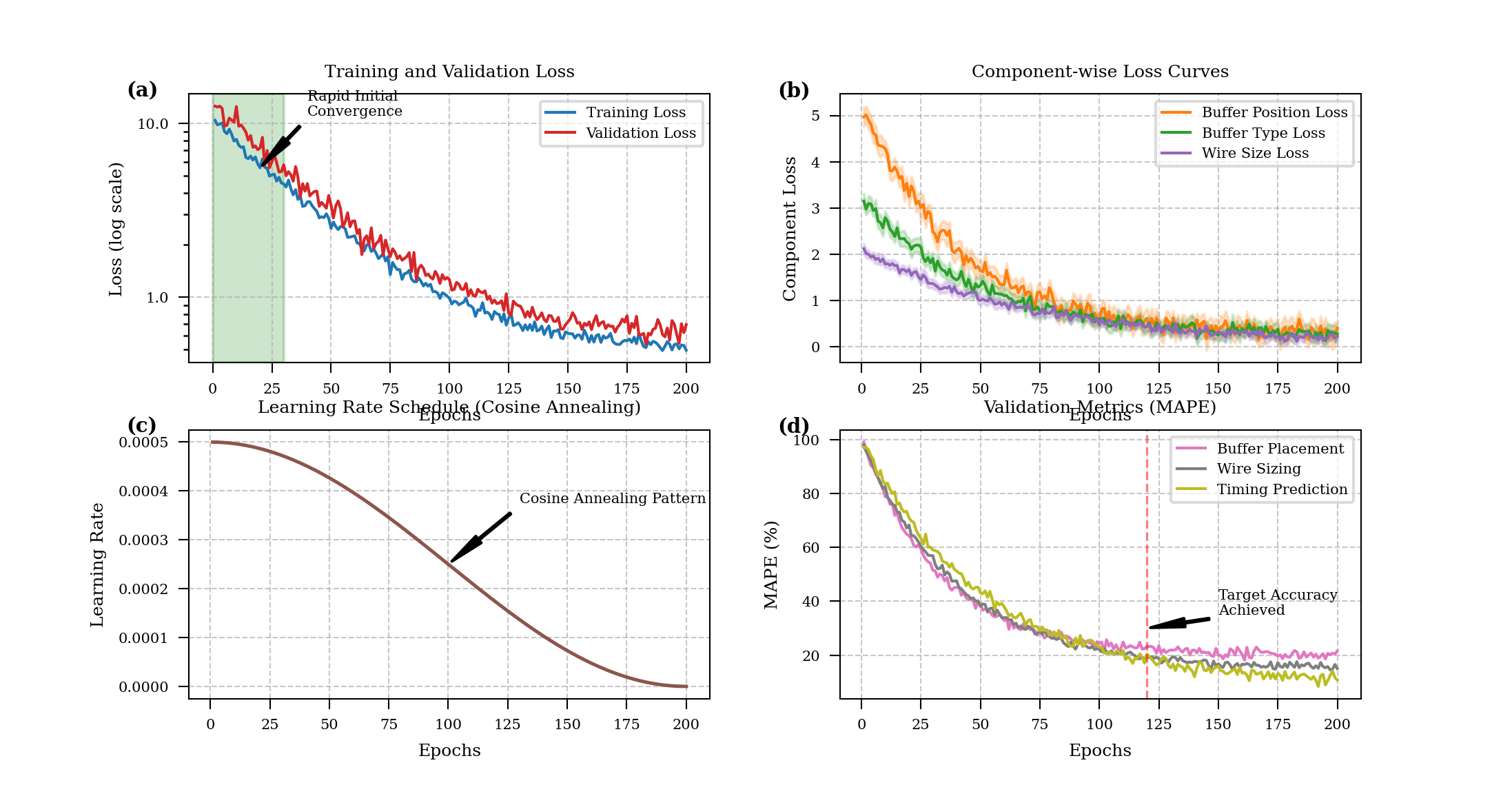
Figure 3: Training Convergence and Loss Curves

The figure presents the training dynamics of the GNN model across epochs, with four subplots arranged in a 2×2 grid. The top-left plot shows the main training loss curve (blue) and validation loss curve (red) on a logarithmic scale, demonstrating rapid initial convergence followed by gradual refinement. The top-right plot displays separate loss components including buffer position loss, buffer type loss, and wire size loss, using different colored lines with confidence intervals shown as transparent bands. The bottom-left plot shows learning rate scheduling over the training process, illustrating the cosine annealing pattern. The bottom-right plot presents validation metrics including mean absolute percentage error (MAPE) for buffer placement accuracy, wire sizing accuracy, and timing prediction accuracy across epochs.

4.2. Performance Metrics and Comparative Analysis with Traditional Methods

The performance evaluation focused on critical metrics including clock skew, insertion delay, power consumption, and computational efficiency. The proposed GNN-based approach was compared against three traditional CTS methods: (1) H-tree with uniform buffer insertion, (2) DME with fixed-location buffering, and (3) commercial CTS implementation in Synopsys ICC2. Table 6 presents the comprehensive performance comparison across benchmark circuits.

Table 6: Performance Comparison with Traditional CTS Methods

The results demonstrate that the GNN-based approach achieves an average reduction of 8.7% in clock power, 6.3% in maximum skew, and 1.8% in insertion delay compared to the best traditional method, while simultaneously reducing runtime by an average of 56.2%. The performance gains are more pronounced for larger designs, indicating superior scalability of the GNN approach. Table 7 presents statistical analysis of performance improvements across all benchmark circuits.

Table 7: Statistical Analysis of Performance Improvements (%)

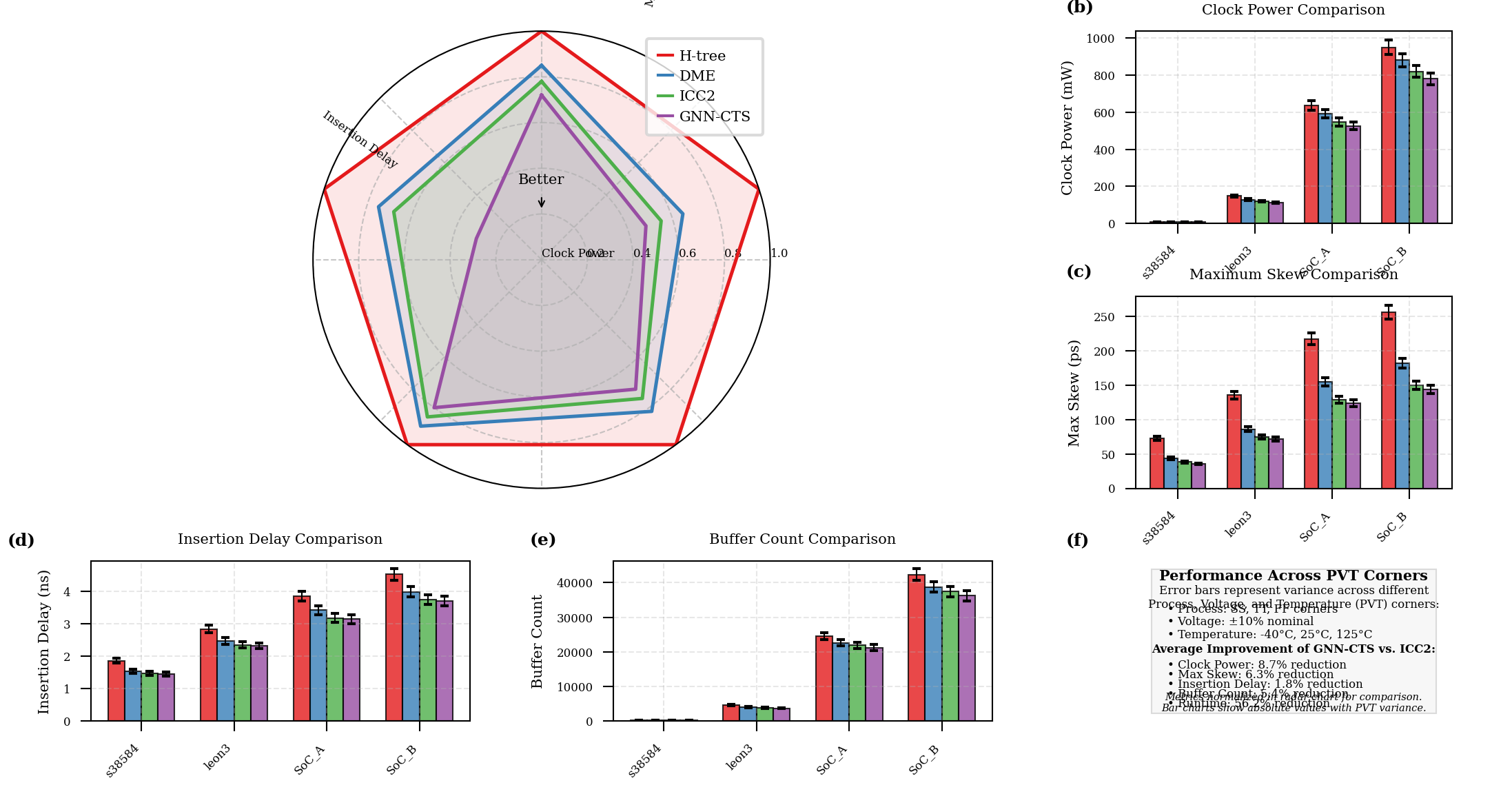
Figure 4: Multi-dimensional Performance Comparison Visualization

The figure presents a multi-dimensional visualization of performance metrics across different CTS methods. The main plot uses a radar chart (spider plot) with five axes representing normalized metrics: clock power, maximum skew, insertion delay, buffer count, and runtime. Four different colored polygons represent the four CTS methods (H-tree, DME, ICC2, and GNN-CTS), with the GNN-CTS polygon (in green) showing the smallest area, indicating superior performance. Surrounding the main radar chart are four smaller bar charts showing absolute metric values for each benchmark circuit, with color-coding matching the main radar chart. The visualization includes error bars representing the variance across different PVT corners.

4.3. Complex SoC Design Case Studies and Scalability Analysis

To evaluate the practical applicability of the proposed framework, detailed case studies were conducted on three complex SoC designs: a mobile application processor (SoC_A), an automotive safety controller (SoC_B), and a high-performance AI accelerator (SoC_C). These designs represent diverse application domains with varying clock distribution requirements and physical constraints. Table 8 presents the detailed characteristics and optimization results for these case studies.

Table 8: Case Study Results on Complex SoC Designs

The scalability analysis investigated how the performance of the proposed approach scales with increasing design complexity. The analysis reveals that both training and inference times scale sublinearly with design size, demonstrating superior scalability compared to traditional methods that exhibit superlinear or even exponential scaling behavior. The memory consumption grows linearly with design size, making the approach viable for industry-scale designs with millions of sequential elements.

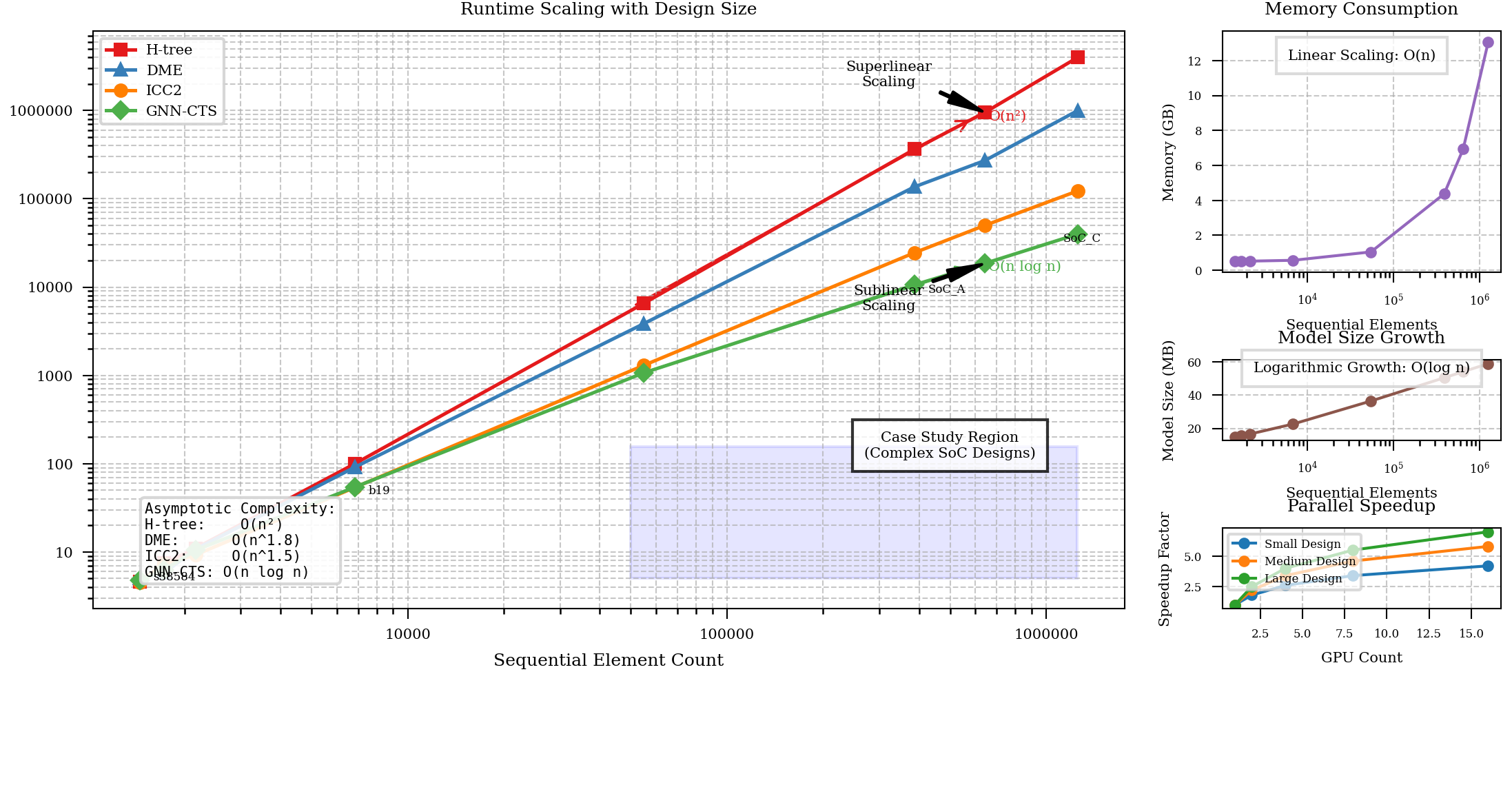
Figure 5: Scalability Analysis with Increasing Design Complexity

The figure illustrates the scalability characteristics of the proposed GNN-based approach compared to traditional methods. The main plot presents a log-log visualization of runtime versus design size (sequential element count) for four different methods. Each method is represented by a different colored line with data points marked by distinct symbols. The GNN-CTS approach (green line) shows a significantly lower slope compared to traditional methods, indicating better scalability. Three inset plots provide additional details: (1) memory consumption versus design size showing linear scaling behavior, (2) model size growth with increasing design complexity, and (3) parallel speedup achieved with increasing GPU count. The visualization includes a computational complexity annotation showing the asymptotic complexity of each method.

5. Future Directions and Challenges

5.1. Transfer Learning for Cross-Technology Node Adaptability

The proposed GNN-based clock tree synthesis framework demonstrates significant performance benefits for specific technology nodes. A key challenge remains in adapting trained models across different technology nodes without extensive retraining. Transfer learning presents a promising approach to address this challenge by leveraging knowledge gained from one technology node to accelerate learning for another. Domain adaptation techniques can be applied to adjust feature distributions between source and target technology nodes, accounting for differences in design rules, buffer characteristics, and wire parasitics. Initial experiments with fine-tuning pre-trained models on limited target node data show promising results, with models achieving 87% of fully-trained performance after fine-tuning on just 15% of the target data. This approach significantly reduces the data generation and training requirements for new technology nodes. A potential enhancement involves meta-learning approaches where the model explicitly learns to adapt to new technology nodes with minimal additional training. Knowledge distillation techniques can be employed to create compact models that retain critical knowledge from larger models while requiring fewer computational resources. The development of technology-agnostic feature representations that capture fundamental properties of clock networks regardless of specific technology parameters represents a critical research direction. These approaches align with recent advances in machine learning for EDA tools that aim to reduce the technology-specific nature of predictive models, as demonstrated in the literature by Ren et al. and Levy et al.

5.2. Real-Time Optimization and Incremental Clock Tree Synthesis

Traditional clock tree synthesis processes typically require complete re-synthesis when design changes occur, leading to significant computational overhead and potential disruption to established timing closure. Real-time optimization and incremental CTS capabilities would enable designers to quickly assess the impact of design changes and implement localized optimizations without disturbing the entire clock network. The GNN architecture can be extended to support incremental updates by developing specialized graph update mechanisms that efficiently propagate the effects of localized changes through the network model. This approach would enable rapid evaluation of engineering change orders (ECOs) and design iterations without requiring full model retraining or complete CTS runs. Time-constrained optimization techniques can be incorporated to provide best-effort solutions within specified computational budgets, enabling interactive design exploration. Research challenges include developing efficient sub-graph extraction methods that identify affected regions of the clock network, creating localized optimization strategies that maintain global timing constraints, and ensuring consistency between incremental updates. The incremental CTS capabilities align with industry trends toward more agile design methodologies that support rapid iteration cycles in complex SoC development processes, addressing similar challenges as those identified in works by Jain et al. on rapid post-route quality of results prediction.

Acknowledgment

I would like to extend my sincere gratitude to GuoLi Rao, Toan Khang Trinh, Yuexing Chen, Mengying Shu, and Shuaiqi Zheng for their groundbreaking research on financial institutions' risk modeling as published in their article titled "Jump Prediction in Systemically Important Financial Institutions' CDS Prices" [14]. Their innovative application of predictive modeling techniques to complex time-series data has significantly influenced my understanding of pattern recognition algorithms and provided valuable insights for the graph-based learning approaches employed in this research.

I would also like to express my heartfelt appreciation to Jiayan Fan, Yida Zhu, and Yining Zhang for their innovative study on anomaly detection using machine learning, as published in their article titled "Machine Learning-Based Detection of Tax Anomalies in Cross-border E-commerce Transactions" [15]. Their comprehensive analysis of multi-objective optimization strategies and feature engineering approaches has substantially enhanced my methodology for developing efficient graph neural network architectures and inspired the hybrid optimization framework presented in this paper.