1. Introduction
In the context of the integration of informatization and distributed computing [1], data resources have become a core element of modern industries, with cloud storage and collaborative modeling being widely applied. Traditional machine learning faces three major challenges [2]: limited cross-institutional data sharing, high risks associated with centralized data processing, and expensive cloud computing costs. In 2016, Google proposed federated learning [3], which avoids direct data transmission and instead exchanges only model parameters, achieving both privacy protection and cross-institutional collaboration. This study optimizes homomorphic encryption to improve computational efficiency and reduce communication complexity. The proposed scheme not only protects privacy but also significantly reduces communication overhead while achieving an accuracy level comparable to traditional federated learning on real-world datasets, demonstrating its practicality and efficiency.
2. Related work
The risk of private data leakage has become increasingly prominent, potentially leading to identity theft, financial fraud, and other security threats. Major global economies have established multi-level regulatory frameworks to address these challenges. In response, the academic community has proposed the integration of homomorphic encryption technology [4], which supports encrypted computations and prevents information leakage during gradient exchange. Federated learning has been applied in various fields, including computer vision, autonomous driving, and natural language processing [5], leading to the development of frameworks such as TensorFlow Federated and FATE [6]. However, it still faces challenges related to communication efficiency, resource imbalances, and vulnerability to malicious attacks. Existing privacy protection methods include differential privacy [7], fully homomorphic encryption [8], and secure multi-party computation [9]. For example, the DSGD algorithm reduces privacy leakage risks [10], Paillier encryption enhances model security [11], and secure aggregation protocols improve robustness [12]. Current research faces major challenges such as data heterogeneity and device resource disparities. Low-quality data may degrade global model accuracy, while existing differential privacy mechanisms have security limitations in non-identity (non-ID) scenarios [13]. Moreover, significant computational power differences among edge devices can affect training efficiency. The FedCS protocol [14] optimizes training through dynamic node selection, but further improvements in resource scheduling strategies are still needed [15]. As an important approach in privacy computing, homomorphic encryption enables secure encrypted computations, enhancing data security. This study focuses on optimizing privacy protection in federated learning through homomorphic encryption, providing technical support for the development of privacy-preserving computing infrastructures.
3. System model and algorithm
To address privacy leakage issues, this paper proposes an improved privacy-preserving federated learning scheme with multi-key aggregation (PFLMA). This scheme optimizes Ring Learning With Errors (R-LWE) homomorphic encryption, improving computational efficiency. Based on the MK-CKKS scheme, it innovatively employs aggregated public key encryption to secure local model parameters. As a result, the cloud server can only decrypt the aggregated result without accessing individual model updates, effectively protecting privacy. Additionally, this scheme resists collusion attacks between participants and the cloud server.
3.1. System model
The PFLMA scheme involves three main entities: the Key Generation Center (KGC), the Cloud Server (CS), and the Participants (P). The system workflow consists of key generation, model training, encrypted transmission, aggregation, and update processes (see Figure 1). The KGC generates public-private key pairs for participants and provides public parameters. Each participant trains a local model and uploads encrypted parameters to the CS. The CS aggregates the encrypted data and distributes the global model. The participants then continue training until convergence.
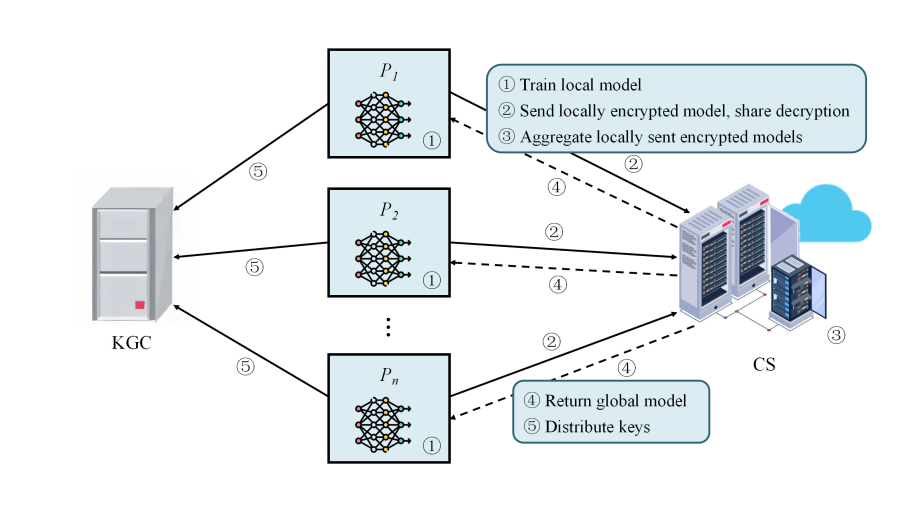
Figure 1. Illustrates the system model of the proposed PFLMA scheme
Key Generation Center (KGC): A trusted third party responsible for generating public parameters, managing key lifecycles, and coordinating secure interactions. The KGC ensures parameter security and supports key updates and revocation.
Participants (P): Data providers that engage in local model training. They encrypt their model parameters using the keys generated by the KGC before uploading them to the CS. The participants optimize their local models while preserving privacy.
Cloud Server (CS): Responsible for coordinating and aggregating encrypted model parameters to generate a global model and distributing it back to participants. The CS does not have direct access to raw data and can only recover encrypted aggregate results.
3.2. Scheme implementation
The PFLMA scheme employs multi-key homomorphic encryption, allowing multiple participants to independently encrypt data and perform collaborative computation, ensuring the secure transmission of model parameters. The scheme improves R-LWE homomorphic encryption, utilizes Stochastic Gradient Descent (SGD) for model training, and incorporates a key management mechanism to ensure privacy security.
3.2.1. System initialization phase
During this phase, the KGC and participants complete system initialization through the following steps:
(1) Initialization: The KGC selects a security parameter, sets \( θ={2^{k}},k≥1 \) , and confirms the key distribution 𝜒 and error distribution \( ψ \) , with ciphertext modulus 𝑞.
The KGC sends public parameters \( pp=(θ,q,χ,ψ,a) \) to the participants.
(2) Encoding and Decoding: Participants expand model parameters into vectors, normalize them, and encode them as polynomials in ring 𝑅.
(3) Key Generation: Each participant \( {P_{i}} \) generates a private key \( s{k_{i}}={s_{i}}←χ \) and an error vector \( {e_{i}}←ψ \) , then computes the public key \( p{k_{i}}={b_{i}}=-{s_{i}}\cdot a+{e_{i}}mod{q} \) . The KGC aggregates the keys to generate a global public key \( pk=\sum _{i=1}^{n}{b_{i}} \) and an aggregated private key \( sk=\sum _{i=1}^{n}s{k_{i}} \) .
3.2.2. Local training phase
(1) Encryption: Participants use SGD to train local models, obtaining model weights \( w_{t}^{i} \) .
The public key \( \widetilde{b} \) encrypts plaintext \( {m_{i}} \) into ciphertext \( c{m_{i}}=({c_{i0}},{c_{i1}}) \) , incorporating randomness \( v←χ \) . The encryption formula is as follows:
\( c{m_{i}}=({c_{i0}}+{c_{i1}})=(v\cdot \widetilde{b}+{e_{i0}}+{m_{i}},{v_{i}}\cdot a+{e_{i1}}). \) | (1) |
(2) Key Switching: Participants compute a transformation key \( {R_{i}}=(-s{k_{i}}\cdot a+sk\cdot a+s{e_{i}})mod{q} \) and perform ciphertext conversion using \( {R_{i}} \) . The transformed ciphertext \( c{m_{i}} \prime \) is then sent to the cloud server.
(3) Homomorphic Addition: The cloud server aggregates all participants' ciphertexts using homomorphic addition, yielding the aggregated ciphertext \( {C_{sum}}=\sum _{i=1}^{n}c{m_{i}} \prime \) , where
\( {C_{sum0}}=\sum _{i=1}^{n}{c_{i0}} \prime \) and \( {C_{sum1}}=\sum _{i=1}^{n}{c_{i1}} \prime \) .
3.2.3. Partial decryption phase
Each participant partially decrypts the aggregated ciphertext using their private key \( {s_{i}} \) , and each participant decrypts the aggregated ciphertext sent by the cloud server, generating the partial decryption result \( {D_{i}}={C_{sum1}}-{s_{i}}\cdot {C_{sum0}}mod{q} \) .
3.2.4. Aggregation phase
The cloud server aggregates the partial decryption results from all participants to recover the plaintext and compute the sum of parameters:
\( \widetilde{m}≈\sum _{i=1}^{n}{D_{i}}mod{q}. \) | (2) |
3.2.5. Model update phase
The cloud server and participants collaboratively update the local training models to derive the final global model. The cloud server computes the weighted average of all participants’ local models to obtain the global model \( {w_{t+1}} \) :
\( {w_{t+1}}=\frac{1}{n}\sum _{i=1}^{n}w_{t}^{i}. \) | (3) |
The cloud server then transmits the updated global model parameters to each participant for the next training round until convergence.
3.3. Security analysis
The PFLMA scheme ensures the confidentiality of model parameters in federated learning, preventing data leakage. The security analysis focuses on the cloud server, participants, and collusion resistance.
(1) Security Against an Honest-but-Curious Cloud Server: The cloud server can only process encrypted data and cannot access any plaintext information. Even after aggregating encrypted data, the server can only obtain the sum, not individual participants’ models or training data.
(2) Security Against Honest-but-Curious Participants: Each participant encrypts its own data, preventing them from inferring others' private information. The encryption randomness and error terms ensure that even if one participant decrypts their data, they cannot obtain others’ information.
(3) Security Against Collusion Between Participants and the Cloud Server: Even if the cloud server and some participants collude, they cannot obtain other participants’ private data. The encryption and randomness mechanisms prevent effective decryption of ciphertext, ensuring data privacy.
4. Experimental analysis
4.1. Experimental setup
The experiments were conducted on a Windows 10 platform, with a hardware configuration consisting of an Intel i5-1035G1 processor and 16GB RAM. The PFLMA scheme was simulated in the context of horizontal federated learning. The experiments utilized two publicly available datasets from UCI Machine Learning Repository: Heart Disease and Pima. The study compared three federated learning approaches:
PFLMA (Proposed Scheme)
Federated Learning Based on MK-CKKS
Unencrypted Federated Learning (UFL)
The evaluation focused on model accuracy and communication overhead.
4.2. Accuracy analysis
The training time of the PFLMA scheme increases as the number of participants grows. Experiments were conducted with different numbers of local training rounds 𝑁, specifically 1, 5, 10, 15, 20, 30, and 40 rounds. The results showed that (see Figure 2 and 3):
When 𝑁=20, the accuracy of PFLMA on the Heart Disease and Pima datasets was 92.73% and 93.37%, respectively. These values were very close to UFL (93.25% and 93.90%), and significantly better than the MK-CKKS scheme.
When 𝑁=40, the accuracy of PFLMA reached 92.89% and 93.87%, which was almost on par with UFL (93.65% and 94.53%) and exceeded the MK-CKKS scheme by 1.25% and 1.89%, respectively.
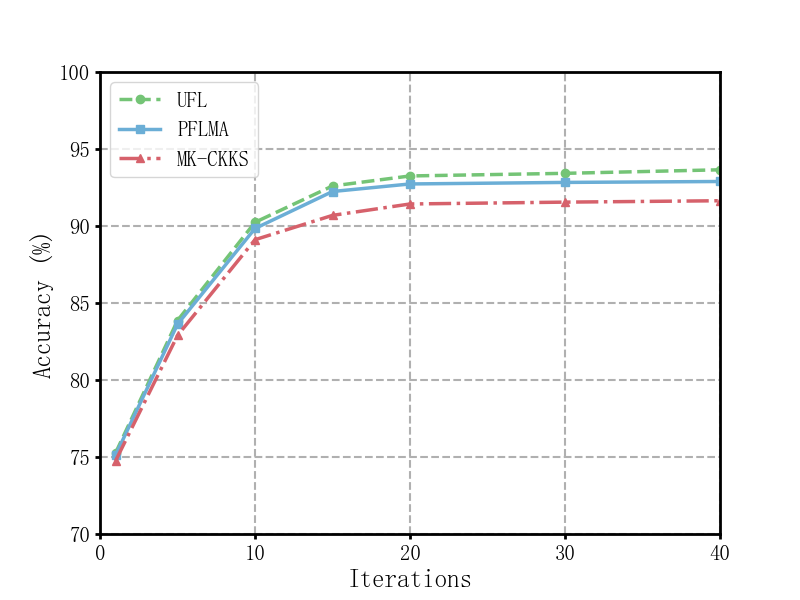
Figure 2. Accuracy on heart disease dataset
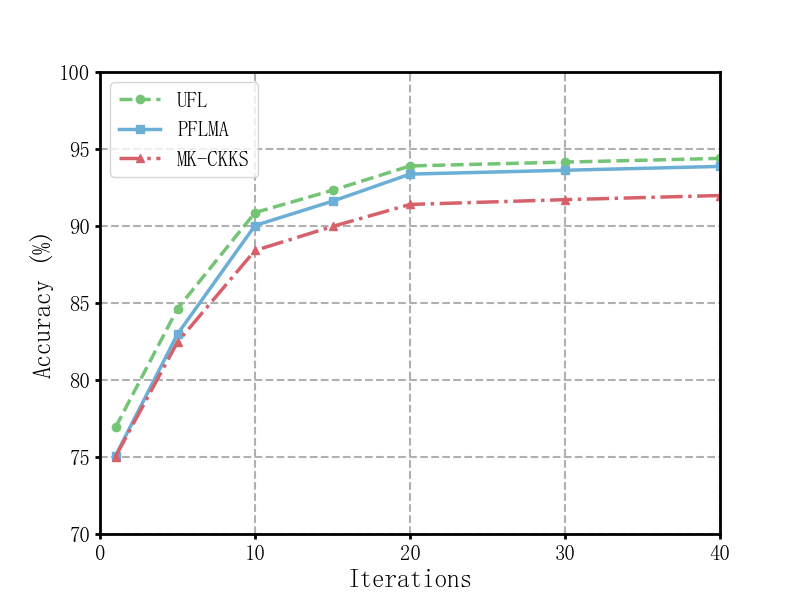
Figure 3. Accuracy on Pima dataset
The results indicate that as the number of training rounds increases, PFLMA achieves accuracy close to UFL while outperforming the MK-CKKS scheme.
4.3. Communication efficiency analysis
Each model consists of 510 weights, with each weight occupying 64 bits, resulting in a ciphertext size of approximately 92KB. The PFLMA scheme introduces additional collaborative decryptions \( {C_{sum1}} \) and \( {D_{i}} \) of 52KB. To reduce communication overhead, experiments were conducted with 10 aggregation rounds or 5 aggregation rounds, allowing convergence to be achieved with 20 or 40 local training rounds, respectively (see Figure 4).
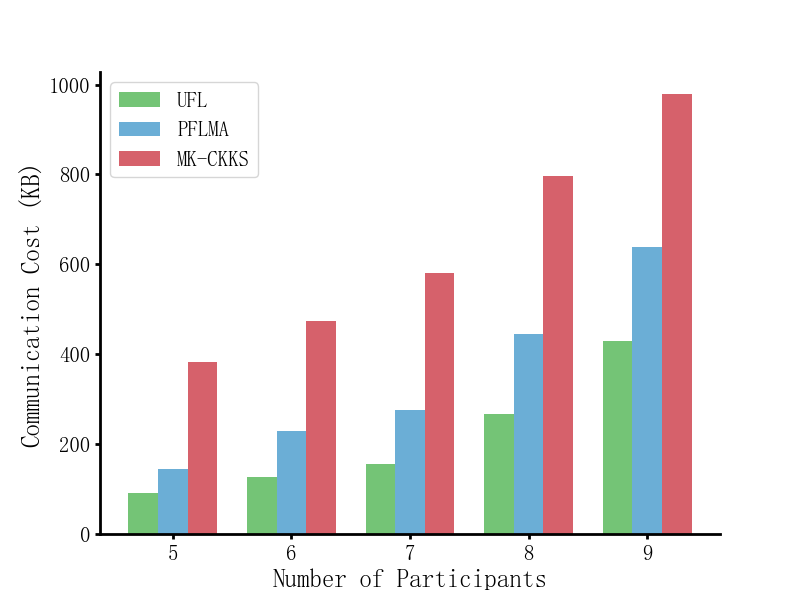
Figure 4. Communication efficiency comparison
The results demonstrate that the communication overhead of PFLMA is slightly higher than UFL but significantly lower than the MK-CKKS scheme. By optimizing computational structures and introducing a trusted key management center, PFLMA reduces both computational complexity and communication costs.
5. Conclusion
This paper proposes an efficient privacy-preserving federated learning scheme based on multi-key aggregation (PFLMA). The scheme improves upon traditional R-LWE homomorphic encryption by simplifying related computations, enhancing computational efficiency and decryption accuracy, and reducing storage complexity during computation and communication, thereby improving overall efficiency. Furthermore, by refining the MK-CKKS scheme, the proposed method defines an aggregated public key and shared decryption mechanism, ensuring parameter privacy during federated learning model updates and effectively preventing collusion attacks between participants and the cloud server. The introduction of a trusted key generation center also minimizes communication overhead among participants. Both theoretical analysis and experimental results confirm that PFLMA effectively preserves data privacy, significantly reduces communication costs, improves efficiency, and performs competitively on real-world datasets.



