Model simulation analysis of superconducting switch applied to high-temperature superconducting electromagnetic suspension magnet

1 Introduction

Maglev trains, operating at high speeds, should aim to minimize the weight of the train body and improve the vehicle’s lift-to-weight ratio [1]. Currently, most onboard HTS (High-Temperature Superconducting) magnets based on ReBCO (Rare-earth Barium Copper Oxide) tapes operate in an open-loop mode, requiring onboard refrigerators and power supplies to maintain the current in the onboard superconducting magnets [2]. The superconducting switch (PCS) is a crucial component for the HTS coil to function in the persistent current mode (PCM) [3-5]. Utilizing superconducting magnet closed-loop operation technology can achieve a mode of operation without onboard power supplies, significantly reducing the weight of the train body. Thermal control superconducting switches are simple to control and do not generate magnetic fields, making them a popular direction in the development of superconducting switches.

A thermal control superconducting switch consists of a non-inductively wound superconducting coil and a heater. By heating the switch locally or entirely through the heater, the temperature of the superconducting switch exceeds its critical temperature, causing quenching and achieving the complete disconnection of the switch [6]. In this paper, a two-dimensional axisymmetric model of a superconducting switch using non-copper-plated stainless steel-encapsulated superconducting tape is established. Under the simulated liquid nitrogen conduction cooling environment, the simulation results show that the switch’s disconnection resistance is 4Ω, and the heater’s heating power is less than 1.15W.

2 Design and establishment of the superconducting switch model

2.1 Design of the superconducting switch

The excitation of a superconducting magnet essentially involves charging an RL circuit, so one important parameter of the superconducting switch is the disconnection resistance, which is the resistance of the switch when it is in a normal state. This resistance value directly affects the excitation efficiency of the magnet [7]. On the other hand, increasing the trigger energy of the heater can theoretically achieve a shorter disconnection time, but the cooling capacity of the conduction-cooled superconducting magnet system is limited. Typically, the second stage cold head of the refrigerator has only about 0.5W of power, making the trigger energy of the heater another critical parameter of the superconducting switch. Therefore, to achieve a higher disconnection resistance, the thickness of the metal layer can be reduced, and the length of the tape wound around the switch can be increased. The parameters of the high-temperature superconducting tape encapsulated in non-copper-plated stainless steel selected for the simulation are shown in Table 1.

Table 1. Geometric parameters of the superconducting tape for simulation

2.2 Establishment of the electrothermal coupled finite element model

The superconducting tape and heating tape are alternately wound in reverse directions, which does not generate a magnetic field, thus ignoring the magnetic field effects [8]. The insulated heating tape is tightly wound in parallel with the high-temperature superconducting tape, ensuring that each turn of the superconducting switch coil is uniformly heated. When the Joule heat generated by the heating tape under trigger energy exceeds the cooling capacity conducted by the refrigerator, the temperature of the superconducting tape will rise. When the temperature of the superconducting layer exceeds the bypass temperature, part of the current in the superconducting layer will flow along the metal layer, generating more heat and causing the temperature to rise rapidly beyond its critical temperature, resulting in the complete quenching of the superconducting tape.

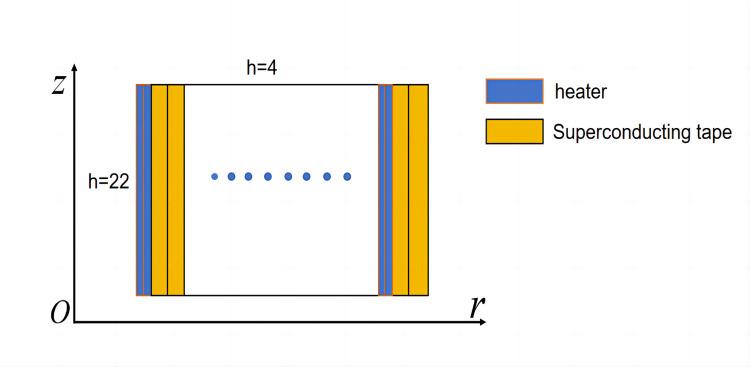
Figure 1. Schematic diagram of the two-dimensional cross-section of the superconducting switch

Using the magnetic field module and the solid heat transfer module of the finite element software COMSOL Multiphysics 6.0, a two-dimensional axisymmetric electrothermal coupled finite element model, as shown in Figure 1, was established to simulate and study the switching time and disconnection resistance under various conditions such as current flow, trigger energy, and cooling environment. On the left side and bottom of the two-dimensional axisymmetric cross-section, the switch coil is in direct contact with the framework, employing the heat flux boundary condition as shown in equation (1). The right side and top surface are in contact with filled paraffin, also using the heat flux boundary condition.

\( n\cdot (k(T)∇T)=h(T-T_{0}) \) (1)

Where h (W/m²·K) is the heat transfer coefficient between the framework and the switch coil, which can be measured experimentally; T₀ is the initial temperature of 77K. The cooling of the superconducting switch coil mainly relies on conduction through the framework. Therefore, in the simulation calculations, h is set to 22 on the left side and bottom surface positions, and h is set to 4 on the right side and top surface to represent the difference in cooling capacity between them.

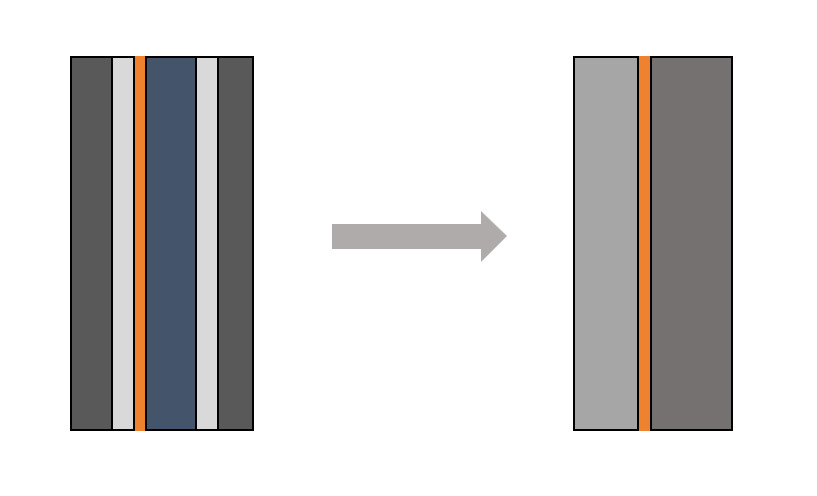
Figure 2. Schematic diagram of the homogenized cross-section of the superconducting tape

YBCO-coated superconducting materials are composite materials with complex structural characteristics such as multilayers and multiple components, among which the aspect ratio of the superconducting layer is extremely high. Therefore, to reduce the computational load and increase convergence, it is necessary to homogenize the model [9]. As shown in Figure 2, the actual superconducting tape can be homogenized into three parts: for the 5mm wide high-temperature superconducting tape, due to the high aspect ratio of the superconducting layer, it can be represented by a straight line. The density and specific heat capacity of the homogenized superconducting layer are averaged based on the mass ratio of each layer of material, as shown in equation (2):

\( ρ_{eq}=\frac{Σρ_{i}\cdot ⅆ_{i}}{d} \) \( C_{eq}(T)=\frac{ΣC_{pi}(T)\cdot ρ_{i}\cdot ⅆ_{i}}{ρ_{eq}\cdot d} \) (2)

Where d is the total thickness of the ReBCO-coated conductor; di is the thickness of the different material layers of the ReBCO-coated conductor; \( ρ_{i} \) and \( C_{pi}(T) \) are the density and specific heat capacity of the i-th layer, respectively. Using the high-temperature superconducting tape parameters shown in Table 1, the homogenized equivalent density \( ρ_{eq} \) on the left is 8734.3 kg/m³ and \( ρ_{eq} \) on the right is 8926 kg/m³, with the equivalent specific heat capacity varying with temperature. The equivalent electrical and thermal conductivity of the homogenized ReBCO-coated conductor in the radial and tangential directions are as shown in equation (3) [10]:

\( σ_{eqr}(T)=\frac{ⅆ}{Σd_{i}∕σ_{i}(T)} \) \( k_{eqr}(T)=\frac{ⅆ}{Σd_{i}∕k_{i}(T)} \)

\( σ_{eqφ}(T)=\frac{Σσ_{i}(T)\cdot ⅆ_{i}}{d} \) \( k_{eqφ}=\frac{Σk_{i}(T)\cdot ⅆ_{i}}{d} \) (3)

Where \( σ_{i}(T) \) and \( k_{i}(T) \) are the electrical and thermal conductivity of the i-th metal layer on the left and right sides of the superconducting layer, respectively, and both vary non-linearly with temperature.

3 Simulation results

The simulation results for a 20-turn high-temperature superconducting coil, with a switch current of 2A and a heating tape power of 1.1W, show the variation of the equivalent metal layer current for each turn of the coil, as illustrated in Figure 3. In the initial triggering phase of the heating tape (0-48s), none of the superconducting tapes quenched, and the current diversion in the equivalent metal layers was almost zero. At around 48.5s, the current in the equivalent metal layers of each turn rapidly increased to the switch current of 2A, and the superconducting switch fully opened within less than 3 seconds. The temperature distribution of the superconducting switch under a switch current of 2A and a heating tape power of 1.15W for the 20-turn high-temperature superconducting coil is shown in Figure 4.

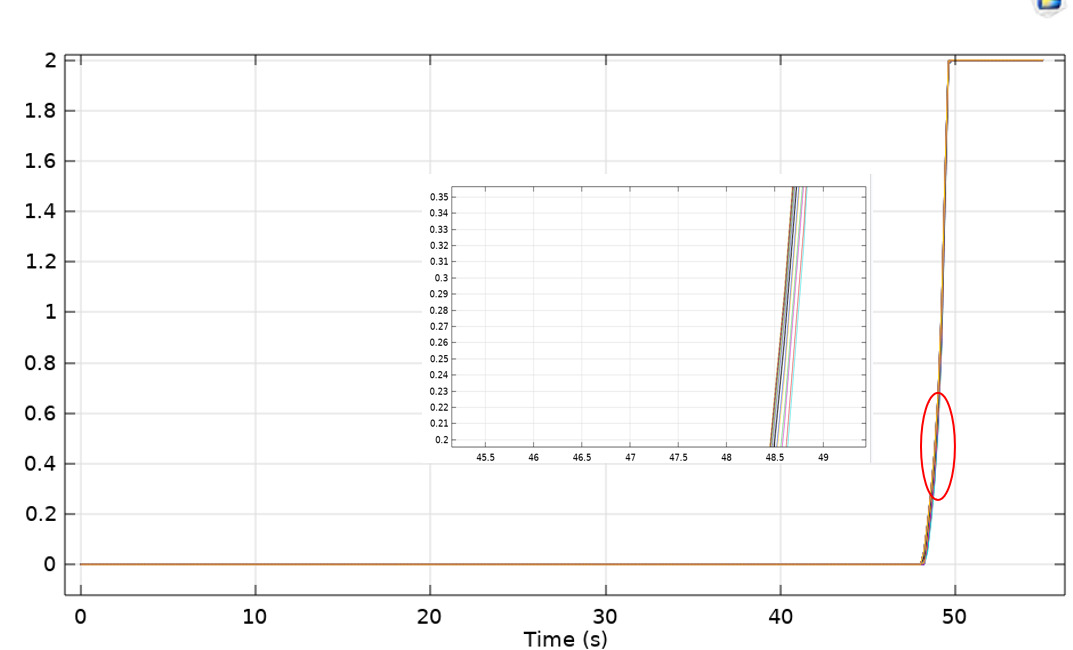
Figure 3. Current in the equivalent metal layer of each turn of the superconducting switch

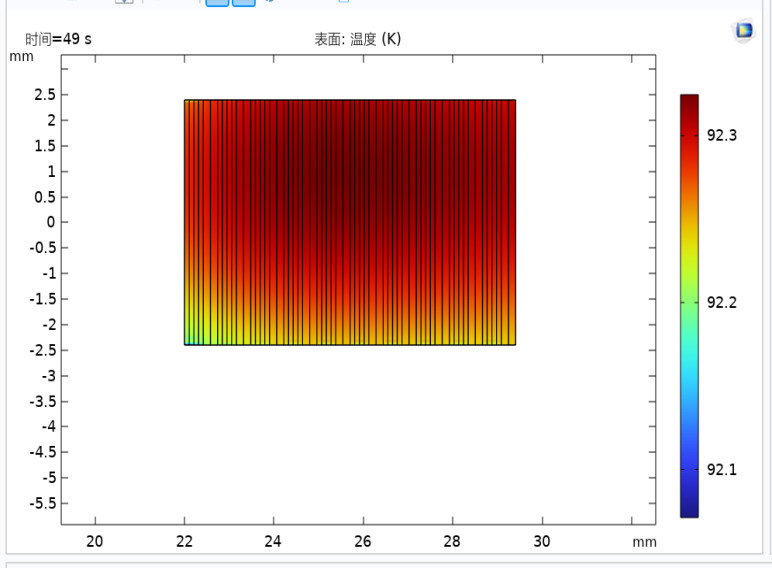
Figure 4. Temperature distribution of the superconducting switch

From Figure 4, it can be seen that the temperature distribution of the superconducting switch is consistent with our observation of the current diversion in the metal layers. From the beginning of heating to the disconnection of the switch, the temperature distribution within the switch cross-section is very uniform. This is because the second-generation high-temperature superconducting tape has a high thermal conductivity in the width direction, as shown in Figure 5, which is obtained under a heating tape power of 1.15W.

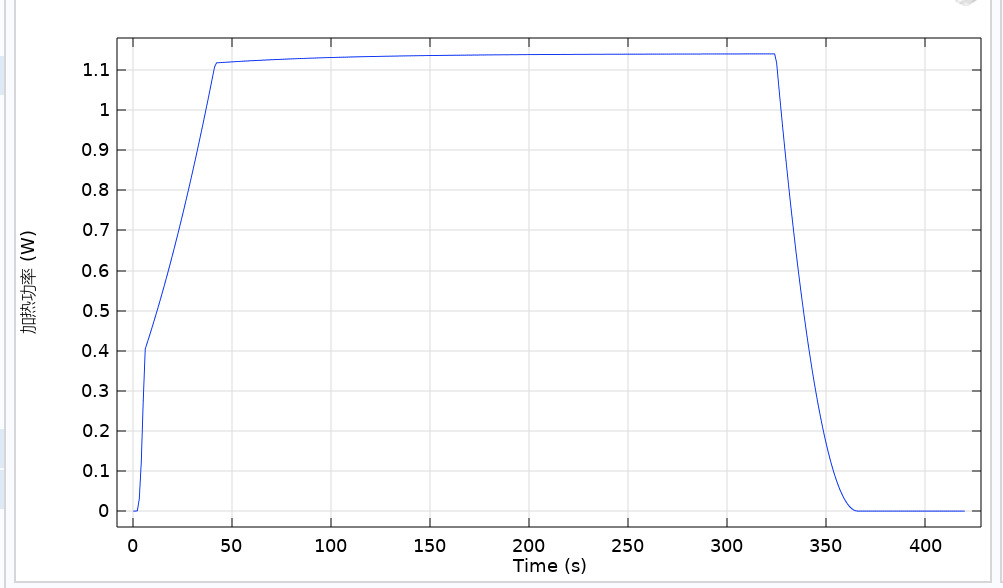
Figure 5. Heater heating power diagram

The simulation yielded the disconnection resistance of the superconducting switch, as shown in Figure 6. The obtained disconnection resistance value is high because we selected superconducting tape encapsulated in non-copper-plated stainless steel, eliminating the copper diversion layer. The resistance during disconnection is mainly determined by the thickness of the stainless steel and the length of the tape.

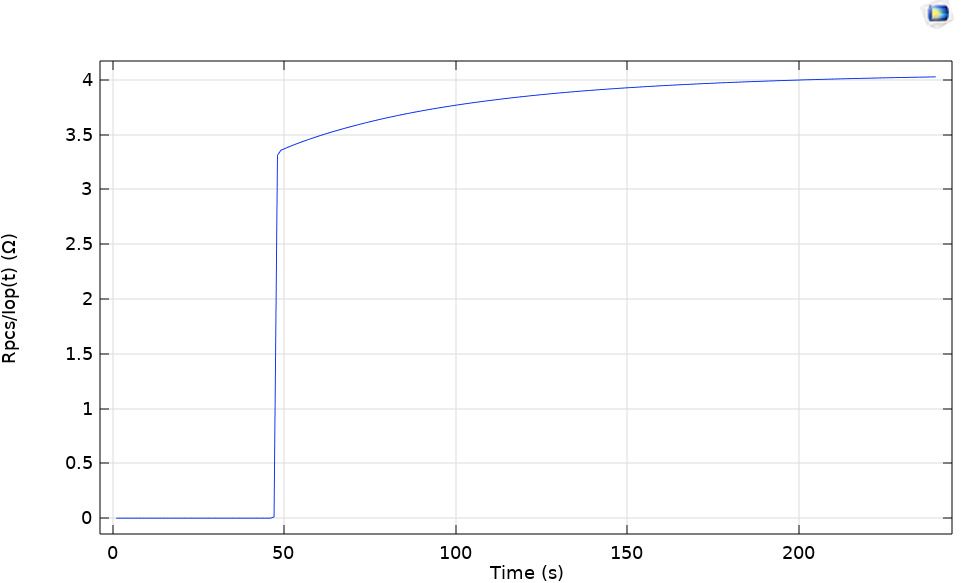
Figure 6. Disconnection resistance diagram of the superconducting switch

4 Conclusion

Through simulation calculations, it is demonstrated that the superconducting switch wound with 5m thin high-temperature superconducting tape encapsulated in non-copper-plated stainless steel achieves a disconnection resistance of nearly 4Ω at a temperature rise of approximately 30K in a simulated liquid nitrogen conduction cooling environment. The simulation results provide useful references for the feasibility of manufacturing pancake-type thermal control superconducting switches. Additionally, several useful conclusions were drawn:

(1) For this special structure of the high-temperature superconducting switch, the current and temperature distribution in each turn of the switch coil is relatively uniform, which can simplify the computational model;

(2) The heating power of the high-temperature superconducting switch is less than 1.2W, and the simulation results meet the application requirements for high-temperature superconducting electromagnetic suspension magnets;

(3) The disconnection time of the high-temperature superconducting switch is mainly determined by the trigger energy of the heating tape and the cooling environment. Further research is needed to determine the cooling boundary conditions that correspond to actual conditions in the calculations.